Geometriai alakzatok
Vizsgáljuk meg, hogy modellünk miként szemlélteti az alábbi - többé-kevésbé - közismert kijelentéseket. Egyenes
 

Két pontra egy és csakis egy egyenes illeszkedik.  

Egy egyenes a síkot két részre  - félsíkokra  - bontja úgy, hogy az egyenesre nem illeszkedő pontok akkor és csak akkor tartoznak  különböző részekhez, ha az egyenes elválasztja azokat.
  Valóban: ha adott a P-modell két pontja, (P és Q), egyértelműen meghatározzák azt az s kört, amely merőlegesen metszi k -t. Az s kör tulajdonképpen a P, Q és a 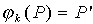  pontokra illeszkedő kör lesz.
 

Van olyan egyenes, amely a sík egy adott pontjára illeszkedik, és egy adott egyenesét nem metszi.
 

Két egy síkban fekvő egyenes lehet metsző, párhuzamos (egyirányú) vagy ultrapárhuzamos (eltérő).
A hiperbolikus sík egyirányú egyenesei a modell olyan - egyeneseket modellező - körívei, (ill. átmérői,) melyek a modell alapkörén érintik egymást.
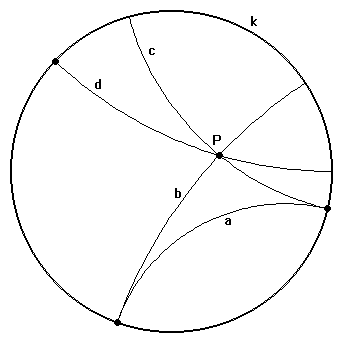Az ábra a egyeneséhez képest b és c egyirányú, d eltérő.
 
 

A sík egy adott pontjára végtelen sok olyan egyenes illeszkedik, amely egy a pontra nem illeszkedő egyenest metsz, végtelen sok olyan is illeszkedik, amely az adott egyeneshez képest eltérő, és ezeket az adott egyeneshez és az adott ponthoz tartozó két egyirányú egyenes választja el egymástól.

Szakasz

Az egybevágósági axiómák egyik lehetséges (és – mint látni fogjuk – praktikus) megadási módja a tér pontjainak a síkra vonatkozó tükrözésére fogalmaz meg axiómákat, melyekből hamarosan eljuthatunk a (síkbeli) tengelyes tükrözésére vonatkozó állításokig. A további (síkbeli) egybevágósági transzformációkat már mint tengelyes tükrözések szorzatait értelmezhetjük.
 

A sík egy egyenese egyértelműen meghatározza a sík önmagára való – tengelyes tükrözésnek nevezett – transzformációját, amely az alábbi tulajdonságokkal rendelkezik: 
 

– az egyenes által meghatározott egyik félsík pontjaihoz a másik félsík pontjait rendeli;    – a képpontokhoz az eredeti pontokat rendeli, azaz involutórikus; – egy egyenes pontjaihoz egyenes pontjait rendeli; 

Két ponthoz egy és csakis egy tükörtengely tartozik, amelyre vonatkozó tükrözés egyiket a másikba viszi.  

Két félegyeneshez egy és csakis egy tükörtengely tartozik, amelyre vonatkozó tükrözés egyiket a másikba viszi. 

Ha egy tengelyes tükrözés az a egyenest a b egyenesbe viszi át, akkor ugyanez a tükrözés az a -hoz szimmetrikus pontokat b -hez szimmetrikus pontokba viszi.
 
A P-modellen a tengelyes tükrözésnek az "egyenest" meghatározó s körre vonatkozó inverzió felel meg. Valóban: ez felcseréli a "félsíkokat", a négyzete az identikus transzformáció, "egyenestartó", hiszen az inverzió kört körbe (vagy az origón átmenő egyenesbe) visz át.

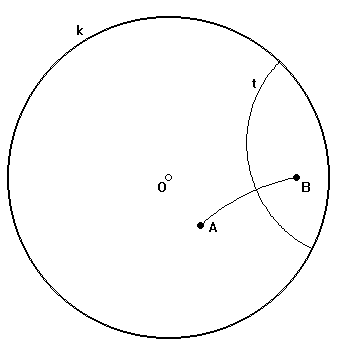
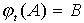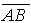Győződjünk meg pl. annak az állításnak a modellbeli helyességéről, miszerint két ponthoz egy és csakis egy tükörtengely tartozik! Legyen adott a P-modell A és B pontja! Az előbb láttuk, miként szerkeszthető a rájuk illeszkedő és k -ra merőleges s kör. Most olyan t kört kell szerkesztenünk, amelyre igaz, hogy , merőleges k -ra, mert "egyenes" és merőleges s -re, mert "az felező merőlegese". (Mivel az inverzió szögtartó, a P - modell is az, tehát a "merőleges egyenesek" a modell merőleges körívei. Könnyen beláthatjuk, hogy a t kör középpontját a k és s körök metszéspontjaira, valamint az A és B pontokra illeszkedő egyenesek metszéspontja adja. (Ha ez nem létezik, akkor t a k alapkör átmérője lesz.)

A programrészlet lényegében " csak" arra képes, hogy szemléltessen egy szakaszt és a szakaszfelező merőleges egyenesét, amely két egybevágó (egyenlő) részre osztja az adott szakaszt.
 

Két szakaszt vagy bármilyen két geometriai alakzatot akkor tekintünk egybevágónak, ha tengelyes tükrözések szorzatával egymásba vihetők.
Itt már érezhetően különbözik a látvány az absztrakt fogalomtól. Ez várható is, hiszen egy egész "sík" -ot egy körlapra zsúfoltunk össze. Minél távolabb van a modell középpontjától a " szakasz" egyik végpontja, annál kisebbnek látszik az egyik fele, mint a másik. Itt jegyezzük meg, hogy a hiperbolikus sík - éppen úgy mint az euklideszi - mindenütt homogén, bár úgy tűnik, mintha a modell középpontjának kitüntetett szerepe lenne. Lehet mondani, hogy ez a modell sajátossága, a modellezés lényegét nem érinti. Két szakasz (a modellen körív) egyenlőségét - egybevágóságát - nem az dönti el, hogy mekkorának látjuk őket, hanem az, átvihetők-e egymásba tengelyes tükrözések (a modellen inverziók) sorozatával.

Lehetőségünk van arra, hogy több szakaszt, ill. ezek felező merőleges egyeneseit is modellezzünk. Ezt kihasználva észrevehetjük, hogy:
 

Egy háromszög szakaszfelező merőleges egyenesei nem biztos, hogy metszik egymást.
Ezzel a kérdéssel azonban részletesebben foglalkozik a következő programrészlet.
 
Három pont Három különböző pontról az alábbi állítások fogalmazhatók meg:
 
Három pontra vagy egy kör, vagy egy egyenes illeszkedik.
Mivel ez az állítás csak az euklídeszi geometriában érvényes, a hiperbolikus geometriában nyilvánvalóan más lehetőségnek is kell lennie. Íme:
 
Három pontra vagy egy kör, vagy egy egyenes, vagy egy paraciklus, vagy egy hiperciklus illeszkedik.
 
Itt eddig nem ismert fogalmakkal találkozunk, amelyek jelentését meg kell világítanunk. Ehhez bevezetjük a sugársor fogalmát, amely - ebben a megfogalmazásban - abszolút geometriai fogalom:
 
A sík egyenesei halmazának egy valódi, nem véges H részhalmazát sugársornak nevezzük, ha bármely két H -beli a és b egyeneshez van olyan H -beli t egyenes, amelyre teljesül, hogy az a és b egyenesek szimmetrikusak t -re, és bármely t Î H egyenesre tükrözve H bármely egyenesét, a tükörkép is H -beli egyenes lesz.
Ebben a definícióban nagy szükség volt mind a valódi, mind a nem véges jelzőre. Ugyanis ha a H halmaz az euklídeszi sík összes egyeneséből, vagy csak három, egy pontra illeszkedő, egymással 60° -os szöget bezáró egyenesből állna, akkor is kielégítené a többi feltételt.
 
Mivel az euklídeszi síkban két egyenes párhuzamos, vagy metsző, ezért kétféle sugársor létezik: az egy pontra illeszkedő egyenesek halmaza, a centrális sugársor, ill. az egymással párhuzamos egyenesek halmaza, a párhuzamos sugársor. 
 
 
A hiperbolikus geometriában - mivel két egyenes kölcsönös helyzete háromféle lehet: metsző, egyirányú (párhuzamos), ill. eltérő (ultrapárhuzamos), ennek megfelelően háromféle sugársor létezik: centrális, egyirányú és eltérő sugársor, amely rendre az egy pontra illeszkedő, a közös végtelen távoli ponttal rendelkező, ill. a sík egy adott egyenesére merőleges egyenesek halmazát jelenti.   
 
 
 
Bármely két egyenes egyértelműen meghatározza a sík egy sugársorát. Ha a sík egy tetszőleges pontját egy sugársor minden elemére tükrözünk, akkor e pont a tükörképeivel együtt egy ún. szabályos görbét, másképpen ciklust alkot, amely a sugársor bármely elemére nézve szimmetrikus alakzat. Egy sugársor minden egyenese merőleges a sugársorhoz tartozó bármely ciklusra. 
Egy centrális sugársor szabályos görbéi koncentrikus körök, melyek közös centruma a sugársor tartója (mind az euklídeszi, mind a hiperbolikus geometriában). 
A centrális sugársor tartóját kivéve a sík minden pontjára egy adott sugársornak pontosan egy egyenese és pontosan egy ciklusa illeszkedik. 
 
 
Az euklídeszi geometria párhuzamos sugársorához tartozó szabályos görbék a sugársor elemeire merőleges egyenesek. 
 
 
 
A hiperbolikus geometria egyirányú sugársorához tartozó szabályos görbék az ún. paraciklusok. Az egyirányú sugársor tartója a sugársor elemeinek a közös iránya. Az eltérő sugársor elemeihez pontosan egy olyan egyenes tartozik, amely a sugársor minden elemére merőleges. (Ez a sugársor tartóegyenese.) A sugársorhoz tartozó szabályos görbék az ún. hiperciklusok. A hiperciklus a sugársor tartóegyenesétől egyenlő távolságra levő pontok mértani helye.

Itt említjük meg, hogy az euklídeszi párhuzamossági axióma ebben a formában is megfogalmazható:
 

Egy félsík pontjai közül a félsík határegyenesétől egyenlő távolságra lévő pontok mértani helye egyenes.

Ez a programrészlet szemlélteti a három, tetszőlegesen megadott ponthoz tartozó ciklust, a három pont által meghatározott három szakaszt, ezek szakaszfelező merőlegeseit, végül az adott pontokra illeszkedő és a kapott ciklusra merőleges egyeneseket. Tapasztalni fogjuk, hogy ez a hat egyenes ugyanahhoz a sugársorhoz tartozik.

A sugársorok és ciklusaik kapcsolatát később részletesebben is meg fogjuk ismerni.

  Mozgó háromszög

Ebben a programrészletben felváltva mozgathatjuk egy háromszög csúcsait. Kétállapotú kapcsolókkal szabályozhatjuk, hogy eközben lássuk-e a háromszög oldalfelező merőleges egyeneseit, magasság egyeneseit és súlyvonalait. A modell alapján megállapíthatjuk, hogy:
 
 

A háromszög oldalfelező merőleges egyenesei ugyanannak a sugársornak az elemei. Ugyanezt állíthatjuk a háromszög magasságegyeneseiről is. A háromszög súlyvonalai egy pontra illeszkednek.

Lehetséges, hogy ez a súlyvonalakkal kapcsolatos állítás többek számára meglepő. Ugyanis a súlypontra vonatkozó tétel legelterjedtebb bizonyítása a hasonlóság fogalmára épül. A hasonlóság pedig csak az euklídeszi geometriában bevezethető fogalom.

A programrészlet kiszámítja a megadott háromszög oldalainak hosszát és szögeinek a nagyságát. A szakaszok mérésével - a távolság fogalmával - később részletesebben foglalkozunk. Most a háromszög szögeiről ejtsünk néhány szót.

A szögfogalom kialakítása, a szögek mérése az abszolút geometria eszközeivel a szokásos módon megoldható. A P-modell már említett előnye, hogy a szögek mérésére, mértékegységeire bevezetett közismert összefüggések a modellen jól tükröződnek: két metsző egyenes szöge egyenlő a modell egyeneseket reprezentáló köríveinek ill. átmérőinek a szögével.

Legendre igazolta hogy:
 

Bármely háromszög belső szögeinek összege kisebb vagy egyenlő az egyenesszögnél. 
A háromszög defektusának (szöghiányának) nevezzük az egyenesszög és a háromszög szögösszegének a különbségét.  

Eszerint Legendre tétele így is megfogalmazható:
 

A háromszög defektusa nem negatív.

Belátható, hogy:
 

Ha egy háromszöget két vagy több háromszögre bontunk, akkor a részháromszögek defektusainak az összege egyenlő az eredeti háromszög defektusával.
 
Legendre azt is megmutatta, hogy:
 
Ha van nulla defektusú háromszög, akkor bármely háromszög defektusa nulla.
 
A defektus fogalmával újabb átfogalmazásait adhatjuk az euklídeszi, ill. hiperbolikus geometria párhuzamossági axiómájának:
 
Van olyan háromszög, amely belső szögeinek összege egyenlő az egyenesszöggel, azaz defektusa nulla. 
Bármely háromszög belső szögeinek összege kisebb az egyenesszögnél, azaz defektusa pozitív.

A háromszög defektusának additív tulajdonsága, miszerint a részháromszögek defektusainak az összege az eredeti háromszög defektusát adja, alkalmas arra, hogy a hiperbolikus geometriában a háromszögek területét a defektusukkal mérjük: 
 

a háromszög területe a defektusának egy (alkalmas) konstansszorosa. 
 
A számítógépi modellünk megengedi azt is, hogy a vizsgált háromszög egy, vagy akár mindhárom csúcsa végtelen távoli pont legyen. Az ilyen, ún. aszimptotikus háromszögnek a végtelen távoli csúcsában mért szöge nulla.
 
Két egyirányú egyenes szöge nulla. Ultrapárhuzamos egyenesek szögét nem értelmezzük.    Ha egy háromszög mindhárom csúcsa végtelen távoli, akkor ennek a legnagyobb a defektusa, ti. az egyenesszög.  

Ez ismét ad egy újabb lehetőséget a párhuzamossági axiómák átfogalmazására:
 

Bármely háromszögnél van nagyobb területű háromszög. 
 
Van legnagyobb területű háromszög. 
    n oldalú szabályos sokszög A szabályos sokszöget egyértelműen meghatározza oldalainak száma, középpontja és egy csúcsa. Ez a programrészlet ezekből az – interaktív módon változtatható – adatokból állít elő szabályos sokszögeket. Megfigyelhetjük, hogy a szabályos sokszög szöge – amely az euklídeszi geometriában csak a sokszög oldalainak a számától függ – itt miként függ a sokszöget meghatározó három adattól.

 

Párhuzamossági szög  
Legyen adott a síkban egy s egyenes, egy attól d távolságban lévő P pont! Legyen továbbá a P pontra illeszkedő és az adott egyenesre merőleges m egyenesnek a P -re illeszkedő e -vel egyirányú egyenessel bezárt szöge d . A d távolságot a P ponthoz és az s egyeneskez tartozó párhuzamossági távolságnak, d -t a P -hez és s -hez tartozó párhuzamossági szögnek nevezzük.

Bolyai János szóhasználatával élve nevezhetjük ezt a szöget az elpattanás szögének is. Ugyanis a P tartójú sugársor egyenesei közül azok, amelyek m-el d -nál kisebb szöget zárnak be, még metszik s -t , az első nem metsző (elpattanó) egyenes éppen a d szög szára.

Ez a programrészlet bemutatja, hogy ez a két mennyiség miként függ egymástól. Ez a kapcsolat - éppúgy, mint a programban bemutatott bármely numerikus összefüggés - nem a modellnek, hanem magának a hiperbolikus sík metrikájának a sajátossága.

   <<<<