Philip J. Davis – Reuben Hersh

Retorika és matematika

     Ha igaz, hogy a retorika a meggyőzés művészete, akkor úgy tűnhet, a matematika ennek épp az ellentéte. Mindezt nem azért szokás így gondolni, mert a matematika nem meggyőző, hanem inkább azért, mert láthatólag nincs szüksége semmilyen művészetre ahhoz, hogy sikerüljön számára a meggyőzés. Minden a tartalomtól függ. A forma részéről elégséges, ha hagyja, hogy a tartalom önmagáért beszéljen.
      Eukleidésznél csak az „általános fogalmak” (az „axiómák” vagy „posztulátumok”) egyszerű kinyilvánításait találjuk, amelyeket egy szigorú és könyörtelen „tétel–bizonyítás–tétel–bizonyítás” láncolat követ. Valóban, a középiskolai geometria-anyagban, amelynek oktatása során Eukleidészt sokmillió iskolásba beleverték, a „bizonyítás” nem volt több, mint egy formális séma, amelyben a két egymás mellett álló oszlop, az „állításoké” a bal oldalon, az „érveké” pedig a jobbon, kérlelhetetlenül elvezetett az „adottól” a „bizonyítandóhoz”, azaz a hipotézisektől a konklúzióhoz.
      A definíciókból és az axiómákból a tétel elkerülhetetlenül következik. Bárki, aki megérti annak kinyilvánítását, el fogja fogadni az igazságát; az egyetértés hiánya ugyanis azt jelentené, hogy az illető inkompetensnek nyilvánítja magát az osztály és a tanár előtt.
      Közismert, hogy a „matematikai bizonyosság” kifejezés a bizonyosságnak azt a fokát jelöli, amelyre más területek legfeljebb csak törekedhetnek. Ennélfogva egy tudomány fejlettségi szintjét annak alapján kezdték megítélni, hogy az milyen mértékben matematizált. Az első helyen a csillagászat, a mechanika és az elméleti fizika többi ága áll. A biológiai tudományok közül a genetika a nyerő, mivel tételei és számításai vannak. Az úgynevezett társadalomtudományok közül a közgazdaságtan az, amelyik a leginkább matematizált, s amely művelőinek a legjobb munkapiacot, valamint a Nobel-díj elnyerésének lehetőségét kínálja.
      Egy tárgyterület számára a matematizáció jelenti az egyetlen lehetséges módját annak, hogy az illető terület a tudomány rangjára emelkedjen. A matematizálás formalizációt jelent, a tárgyterület axiomatikus felépítését, s ezáltal – a feltevés szerint – a retorika rontásától való megtisztítását. Megtisztítást ama – jogászokra jellemző – fogásoktól, melyeket leginkább azok használnak, akik nem hagyják, hogy a tények és a logika önmagukért beszéljenek. Azok szemében, akik szembeszállva e dogmával, azt kívánják hangsúlyozni, hogy a retorika az összes emberi törekvés szükségszerű és érvényes aspektusa, a matematika sárkányként jelenik meg, melyet el kell pusztítani.
      Jelen cikknek mármost az a szándéka, hogy gyengítse a matematizálás iránti ilyetén igényeket. „Gyengítésről” beszélünk, nem „elvetésről” vagy „lerombolásról”, hiszen mindannyian tisztában vagyunk azzal, hogy a matematizálásra vonatkozó igények nem ok nélkül merülnek fel. Ezek érvényessége azonban korlátozott. A matematikai elméletekre éppoly szkepszissel kell tekintenünk, mint a „hétköznapi nyelven” megfogalmazottakra.
      A mi célunk annak megmutatása, hogy a matematika valójában nem is az ellentéte a retorikának. Inkább arról van szó, hogy a retorika néha matematizált, a matematika pedig néha retorikus lehet. Az első feladatunk az lesz, hogy kimutassuk (ami egyébként már általánosan elfogadott nézet): a matematika nyelve, a matematika díszítményei a különféle célok megvalósítása során s különösen az úgynevezett viselkedéstudományok területén retorikai eszközként használatosak. A második s egyben nagyobb feladatunk annak megmutatása, hogy a matematika gyakorlatában hivatásos matematikusok között a tisztán formális vagy logikai elvárások mellett folyamatos és nélkülözhetetlen szerepet játszanak az érvelés és meggyőzés retorikus módozatai.

A matematika mint retorika

     Általánosan elfogadott az a nézet, hogy a matematikának két ága van: a tiszta és az alkalmazott matematika. Mi szeretnénk megmutatni, hogy három ága van: a tiszta matematika, az alkalmazott matematika, valamint a retorikus matematika.
      A tiszta matematikához tartozik a számelmélet, a geometria, az algebra vagy az analízis. Ez az, amit a matematikusok saját kedvükre vagy egymás örömére művelnek. Ha elégedettek azzal a móddal, amely révén valamire megoldást találnak, gyakran azt mondják, hogy az illető meglátás elegáns vagy mély. Mit jelentenek ezek a szavak? Nos, a „mély” azt jelenti: bonyolult, nem nyilvánvaló, valami, ami számos, a felszín alatt húzódó réteg feltárására vár. Az „elegáns” jelentése pedig: meglepő, váratlan, valamely szellemes eszköz vagy éleselméjű ötlet révén viszonylag kevés munkával jelentős eredményekre vezető.
      Második kategóriánk – az alkalmazott matematika – az a tudomány, amelyet a matematikusok a célból művelnek, hogy megoldják a társadalom által kitűzött bizonyos feladatokat. Ilyen feladat az időjárás számszerű előrejelzése, az elektromosizzó-gyártás statisztikai minőségellenőrzése vagy egy Szaturnuszra induló rakéta röppályájának megtervezése. Napjainkban a feladatok megfogalmazója és finanszírozója egyre inkább a hadsereg, s e feladatok közé tartozik a felkészülés az élet idő előtti megszűnésére e bolygón.
      Végül létezik retorikai matematika. Mit is takar ez a kifejezés? Ez az a fajta matematika, amely se nem tiszta, se nem alkalmazott. Nem tiszta, mivel e területen egyetlen matematikailag értékelhető eredmény sem születik, egyetlen új matematikai ötletet sem vetnek fel, egyetlen matematikai problémát sem oldanak meg; s nem is alkalmazott, mivel itt nincs szó semmilyen, a való világra vonatkozó következményről. A retorikai matematikából – eltekintve a publikációktól, a beszámolóktól és a támogatási javaslatoktól – semmilyen praktikus eredmény nem származik. A „retorikai” szó több dolgot jelent. Sértő, pejoratív jelentéseinek egyike szerint: üres szócséplést vagy harsány ködösítést. A matematika lehet retorikus a szónak ebben az értelmében. Az ilyet retorikai matematikának nevezzük.
      Felállíthat például egy nemzetközi konfliktust szemléltető „matematikai modellt”. Lehet, hogy a modell csupán axiómák egy sora: axiomatikus modell. Lehet továbbá stratégiák valamely együttese az ezekhez rendelt eredmény-mátrixszal: egy játékelméleti modell. De éppígy lehet „állapotváltozóknak” valamilyen együttese is, melynek révén részletesen meghatározzák a nemzetközi katonapolitikai helyzetet néhány olyan egyenlettel együtt, amelyek összefüggést teremtenek az állapotváltozók mai és holnapi értékei között. Táplálja be ezt a számítógépébe, s máris egy szimulációs modellt kapott.
      Igazából nem érdekes, milyen módon jár el. Megtervezheti, közzéteheti, kiigazíthatja a modelljét (vagy kidobhatja, s kezdheti újra a semmiből), újratervezheti, újra közzéteheti azt.
      Miért nem alkalmazott matematika az ilyen tevékenység? Az alkalmazott matematikáról alkotott szokásos elképzelés, amellyel számos tankönyv első oldalán találkozhatunk, három fázisra bontja az alkalmazott matematikus munkáját, amely sematikusan ábrázolható egy nyíl-diagramon (1. ábra). A felső szint az elmélet; az alsó a fizikai realitás. A való világ problémáinak matematikai tanulmányozása (megkülönböztetve a tiszta matematikában felmerülő problémáktól) matematikai modellalkotással kezdődik. Mindez nem jelent mást, mint hogy a fizikailag releváns mennyiségeket matematikai – rendszerint numerikus, néha azonban nem numerikus: például geometriai vagy logikai – változókkal helyettesítik, és a fizikai tapasztalat alapján megállapítják az e változók között fennálló relációkat – többnyire algebrai és differenciálegyenleteket, illetve egyenlőtlenségeket. A második lépés, a matematikai elemzés fázisa, bizonyos esetekben lehet az egyenlet megoldása, egy explicit képlet kialakítása valamely változóra, például a hőmérsékletre, a népesség nagyságára, vagy egy bolygó helyzetére. Más esetekben előfordulhat, hogy nem adható explicit megoldás. Bizonyos közelítő vagy kvalitatív következtetésekhez azonban matematikai okoskodással lehet jutni; például, hogy a bolygó a Naptól számítva egy bizonyos távolságon belül marad; hogy a lakosság száma előbb gyors növekedésnek indul, majd egyensúlyba kerül, s egy adott határértékhez közelít; vagy hogy a hőmérséklet szabályos és monoton összefüggést mutat a közeg diffuzivitásával.
      A szigorú matematikai érvelésen kívül a második lépés ad hoc egyszerűsítéseket is magában foglalhat; például bizonyos változók konstansokkal való helyettesítését vagy néhány „mellékes” terminus kiküszöbölését az egyenletekből. E lépéseket néha fizikai megfontolások igazolhatják; máskor ezek csupán olyan kísérletképpeni próbálkozások, melyeknek érvényessége a végeredmények fényében döntendő el. A második lépéshez rendszerint számítógépes kalkuláció is tartozik. Egy számítógépes program elkészítéséhez, mely a valós világ valamely problémájának elemzésére szolgál, előzőleg be kell vezetni a kérdéses probléma modellálására alkalmas változókat és relációkat. A számítógépes kalkuláció néha olyan munkamegtakarító eszköz lehet, amely a gondolkodást és az emberi elemzést helyettesíti. Többnyire azonban egy bizonyos mértékű gondolkodásnak meg kell előznie a kalkulációt, ha nem akarjuk, hogy ez utóbbi ilyen vagy olyan formában céltalanná és haszontalanná váljon.
      A harmadik lépés – a matematikai vagy számítási eredményeknek a valós világ terminusaiban történő értelmezése – különféle formákat ölthet. Az értelmezés lehet predikció, amely szerint a vizsgált rendszer egy adott módon fog viselkedni. Lehet magyarázat, amely azt mutatja meg, hogy bizonyos okok előidézhetnek (vagy nem idézhetnek elő) bizonyos hatásokat. Az egész modelláló és elemző eljárásnak az értéke mindenesetre egészen addig meghatározatlan marad, amíg az értelmezést – a harmadik lépés végeredményét – megfigyelés vagy kísérlet útján, a valós világ adatainak fényében le nem ellenőrzik. Egy modell alkalmassága vagy érvényessége mindenekelőtt az első lépésben megfogalmazott feltételezések inherens ésszerűségétől vagy plauzibilitásától függ; másodsorban a modell hajlékonyságától, attól, hogy a második lépésben elvégezhetőek-e olyan matematikai műveletek, amelyek valamelyest újszerű és érdekes következményekhez vezetnek; végül pedig, a harmadik lépésben, az eredmények illeszkedési fokától, attól, hogy milyen mértékben igazodnak az elméleti eredmények a valós világ adataihoz.
      E „Tanuljunk könnyen, gyorsan…” típusú tudományos módszertan kritériumokat próbál adni, melyek alapján megítélhetőek azok az igények, amelyek valamely tárgyterületen a matematika alkalmazására irányulnak. A háromlépcsős paradigma konvencionális, s talán valamelyest leegyszerűsítő. Lehetséges, hogy a kutatás bármely konkrét szakasza a három közül csak az egyik lépésre korlátozódik, vagy hogy a három lépés egymás után többször is megismétlődik, ahogyan egy modellt annak kidolgozói fokozatosan finomítanak és korrigálnak. Továbbá, esetenként előfordulhat, hogy nem lehetséges vagy nem célszerű egyértelműen elhatárolni az egymást követő lépéseket.
      Mindezt figyelembe véve vannak bizonyos kritériumok, melyek alapján a matematikus eldönti, vajon a matematika „alkalmazása” valódi vagy látszólagos:
     – Igazolja-e a valós világban mutatkozó probléma mélysége a matematikai modell komplexitását?
     – Vannak-e olyan valódi matematikai érvek vagy nem-triviális számítások, melyekhez szükség van a javasolt matematikai modell eszköztárára?
     – Meghatározhatóak-e értelmesen és a kellő szabatossággal az egyenletekben szereplő együtthatók és paraméterek?
     – Ellenőrizhetőek-e a következtetések a valós világ adatainak fényében? Van-e valamilyen nem-nyilvánvaló következménye az elemzésnek?
      A matematikai módszerek bevezetését a közgazdaságtanba, pszichológiába, valamint az úgynevezett viselkedéstudományok egyéb ágaiba mindig heves viták kísérték. A matematizálás ellenzőinek jó okaik lehettek az ellenállásra. Érveik erejét azonban jelentős mértékben csökkentené, ha felmerülne annak a gyanúja, hogy nem értették meg a kifogásolt matematikai módszereket. Ezért fontos világosan leszögezni, hogy a viselkedéstudományok matematikájával kapcsolatos szkepticizmus sokkalta erősebb a hivatásos matematikusok, mint a nem matematikai jellegű viselkedéstudományok művelői körében.
      E szkepticizmust nyomtatásban ritkán szokás megfogalmazni. Szemben a filozófusokkal és az irodalomtudósokkal, a matematikusok nem igazán kedvelik a vitát. Nincsenek hozzászokva s rendszerint inkább csöndben maradnak, csak hogy elkerüljék. (Nevezetes példa erre az az eset, amikor Gauss titokban tartotta a nem euklideszi geometriára vonatkozó felfedezését, mivel félt a „boeociánusok”1 zúgolódásától.)
      Létezik egy további indok, amiért mi, matematikusok, ritkán fogalmazzuk meg nyomtatásban a viselkedéstudományok matematikájára vonatkozó szkepticizmusunkat: tisztában vagyunk azzal a ténnyel, hogy bizonyos esetekben haszonnal járhat a matematika efféle alkalmazása. Ezért nem ítélhetjük el annak minden formáját. A gyakorlatban meddő vállalkozás lenne a búzát és a pelyvát elválasztani egymástól. Következésképpen semmit sem mondunk. Annak az embernek a háta mögött azonban, aki a matematikai pszichodinamikáról beszél, értetlenkedő pillantást vetünk egymásra, és megvonjuk a vállunkat.
      Az a tudat, hogy a matematikusok is osztják e véleményt, talán erősíteni fogja az elszántságot mindazokban, akik tagadni kívánják a retorikai matematika létezését. Ha tanácsra vagy bátorításra lenne szükségük egy hivatásos matematikus részéről, nem kell messzebbre menniük saját egyetemük matematika tanszékénél. Keressék csak meg az általuk elérhető legjobb matematikust! Mindegy, hogy az illető személy tiszta vagy alkalmazott matematikával foglalkozik-e; a lényeg, hogy a matematikával szemben magas szintű elvárásai legyenek.
      A retorikai matematikáról alkotott negatív meghatározásunkat újrafogalmazhatjuk pozitív terminusokban. A retorikai matematika az akadémikus szellemi csatározások egy formája. Mindenekelőtt szorosan összefügg azzal a magas presztízzsel, amelyet a XX. századi Észak-Amerika kölcsönzött a matematikának. A retorikai matematika látszólag olyan, mint az alkalmazott matematika. Mindazonáltal könnyű őket megkülönböztetni egymástól. Az alkalmazott matematika előbb vagy utóbb valamilyen kísérlethez vagy méréshez vezet. Az alkalmazott matematika művelése vagy a kezdet kezdetén vagy legvégül visszavezet a modellálni kívánt jelenséghez. A retorikai matematika gyakran elvileg is alkalmatlan rá, hogy összevessék a valósággal. Lehetséges például, hogy a modell olyan numerikus paramétereket tartalmaz, amelyeket nyilvánvalóan lehetetlen megmérni (példa erre egy nemzetközi konfliktus modellje, amelynek együtthatói a nagyhatalmak „agresszivitásának” mértékével egyenlőek).
      Szórakoztató példával állt elő Neal Koblitz „Mathematics as Propaganda” című tanulmányában. Idézetei a jelentős tekintélynek örvendő Samuel Huntington Political Order in Changing Societies című, a fejlődő országok problémáinak témakörében meghatározó jellegű munkájából származnak. A könyv 55. oldalán három egyenlőtlenség található, amelyek néhány társadalmi és politikai fogalmat hoznak egymással összefüggésbe:

     Miként azt Koblitz is megjegyzi, „Huntington egyszer sem érzi szükségesnek, hogy tájékoztassa olvasóját, vajon milyen értelemben nevezhetők a fenti összefüggések egyenleteknek. Kétséges, hogy az (a) – (g) terminusok bármelyike is mérhető mennyiségre vonatkozna és egy adott numerikus értékkel rendelkezne. Mik a szóban forgó mértékegységek? Vajon Huntington egyetértene-e velünk, ha a kilenc jegyű algebra technikáival műveleteket végeznénk ezeken az egyenleteken? Ha igen, akkor például az alábbi következtetésre juthatnánk

a = bc = bde = bdfg,

azaz »a társadalmi mobilizáció egyenlő a gazdasági fejlődésnek, a mobilitási lehetőségeknek, a politikai intézményrendszer fejlettségének, valamint a politikai labilitásnak a szorzatával!«” (Korbitz 1981, 55).

Retorika a matematikában

     A retorikus matematikáról most áttérünk a matematikai retorikára. Szeretnénk szemügyre venni néhány matematikai megnyilatkozást, illetve írásművet (matematikusok szóbeli vagy írásbeli megnyilvánulásait, amikor matematikusként a munkájukat végzik), és megnézni, hogy milyen retorikai aspektusokat tudunk azonosítani ezekben.
      Ha a retorika szokásos definícióját tartjuk szem előtt, mely szerint az olyan természetes diskurzus, amelynek célja a meggyőzés, akkor a retorika a matematikában nem lenne más, mint a meggyőzésünk szolgálatába állított köznyelv – valamilyen matematikáról szóló állítás érvényességére vonatkozóan. Mi az, ami mellett alkalmasint retorikai érveket hoznánk fel? Bizonyára szívesen érvelnénk a matematika hasznossága mellett annak különféle alkalmazásaiban. A matematika filozófiája szintén retorikai argumentáció révén épül fel. A matematikai igazság azonban – visszalépve egy szinttel az igazságról folyó eszmecserétől magához az igazsághoz – az általános vélekedés szerint olyan eszközök segítségével állapítható meg, amelyek a retorikának épp az ellentétét jelentik. Az osztályteremben, a tankönyvben és egy sor filozófiai írásműben egyaránt hangoztatott tézis szerint a matematikai igazság megállapítására egyetlenegy érvelési mód áll rendelkezésre, amelynek lényege, hogy a hipotézistől a konklúzióig olyan apró logikai lépések sorozatán keresztül jutunk el, amelyek mindegyike elvileg mechanikusan végrehajtható. T.O. Sloane a következőket írja („Rhetoric”, in Encyclopaedia Britannica): „Minden megnyilatkozás, eltekintve talán a matematikai képlettől, egy adott közönség adott helyen és időben történő befolyásolására irányul.” A matematikai kijelentések, úgy tűnik, kivételt jelentenek e szabály alól. A Sloane professzor szavai mögött érezhető enyhe kétely azonban jelentős mértékben növelhető. A matematikai bizonyításnak megvannak a maga retorikai indítékai és a maga retorikai elemei.
      Tegyük fel, hogy belehallgat egy egyetemi matematikaórába, amely elég magas színvonalú ahhoz, hogy a tanár komoly súlyt helyezzen a matematikai bizonyításra. Képzeljük el, hogy pont egy ilyen bizonyítás kellős közepén kapcsolódik be az előadás menetébe. Elméletileg éppen azoknak az apró logikai átalakításoknak a bemutatását kellene hallania, amelyek könyörtelenül elvezetnek a hipotézistől a konklúzióig. Az ön által hallottak egy része valóban egy efféle litánia lesz. Bizonyos azonban, hogy közbevetőleg más megfogalmazások is elhangzanak: „Könnyű belátni, hogy...” – „Egy nyilvánvaló általánosítás segítségével...” – „Egy hosszú, de elemi számítás, melynek végrehajtását a hallgatókra bízom, igazolni fogja, hogy...”
      Ezek a fordulatok nem képeznek bizonyítást: ez a bizonyítás szolgálatába állított retorika. A matematikus- és informatikus-hallgatók körében nemrég kézről kézre járt egy mókás kivonat, mely a bizonyítást helyettesítő retorikai eszközöket tartalmazott. Felidézünk néhány sort e munkából, amelyet egyébként Dana Angluin állított össze a Yale Egyetem Informatikai Tanszékén.

Hogyan bizonyítsunk?

Bizonyítás példa segítségével:

A szerző csak az n = 2 esetet vizsgálja meg, s azt állítja, hogy az tartalmazza a teljes bizonyításhoz szükséges megfontolások nagy részét.

Bizonyítás megfélemlítés révén:

„Triviális.”

Bizonyítás kiemelkedő tekintélyre hivatkozva:

„A liftben összefutottam Karppal és azt állította...”

Bizonyítás egy nehézkes jelölésrendszer segítségével:

A legjobb, ha legalább négy ábécét és további speciális szimbólumokat alkalmazunk.

És így tovább egészen a huszonnegyedik kategóriáig.

     Felhozható az az ellenvetés, hogy az összes ilyen retorikai hókuszpókusz, az intuícióra, különféle képekre, metaérvekre, a cáfoló evidenciák hiányára, még meg nem jelent cikkek eredményeire való hivatkozás, csak az előadó vagy a szerző pongyolaságát tanúsítja. A matematikai irodalomban megjelenő minden egyes tétel mögött valahol ott kell állnia a hipotézistől a konklúzióig elvezető, abszolút világosan felfogható, a terület szaktekintélyei által hitelesített, a kezdők által is igazolható s az egész matematikus közösség által elfogadott logikai átalakítások sorozatának. E benyomás abszolút mértékben téves. Ennek ellenére általánosan elfogadott mindazok körében, akiknek nem a matematika a hivatása. A matematikus-hallgatók néha egészen addig a fejükben hordozzák ezt a képet, amíg maguk is el nem mélyednek valamely kutatásban; ilyenkor rendszerint hirtelen és váratlan megdöbbenéssel veszik tudomásul, hogy a matematika valódi világa távolról sem hasonlít az ideálisra.
      A matematika valódi világában egy matematikai cikk két dolgot mutat meg. Egyrészt tanúsítja, hogy a szerzőnek sikerült meggyőznie magát is és baráti körét is bizonyos „eredmények” igazságáról, másrészt bemutatja azoknak az evidenciáknak egy részét, amelyeken a fenti meggyőződés nyugszik.
      Részeket közöl, nem mindent, mivel bizonyos „rutinszámításokat” nem tartanak érdemesnek kinyomtatni. Az olvasótól rendszerint elvárják, hogy önmaga számára felidézze ezeket. Sokkal fontosabb, hogy bizonyos „heurisztikus” okfejtéseket, beleértve talán a vizsgálódás megkezdését előmozdító legfőbb megfontolásokat, a publikálás szempontjából „lényegtelennek” vagy „irrelevánsnak” szoktak tartani. E háttérben meghúzódó, közzé nem tett motívumok ismerete szükséges feltétele annak, hogy valaki a cikk értő olvasójának számítson.
      De hogyan sajátítjuk el ezt a hátteret? Majdnem mindig élőszóban, a megcélzott közönség valamely másik tagjától, egy, az adott konkrét kutatási területre korábban már bevezetett másik személytől.
      Mit jelent továbbá egy matematikus esetében, hogy meggyőződött bizonyos eredmények igazságáról? Más szóval, miben áll a gyakorló matematikus által ilyenként elismert matematikai bizonyítás? Bármilyen zavaró és meghökkentő, az igazság az, hogy semmilyen explicit válasz nem adható e kérdésekre. A formális logika felől nézve mindegyik bizonyítás tökéletlen. Hogyan döntjük el, hogy e tökéletlen bizonyítások közül melyek helytelenek s melyek helyesek a szónak abban az értelmében, hogy azok a képzett szakemberek számára meggyőzőek és elfogadhatóak?
      Ez csak a kérdéses matematikai elmélet elsajátítása révén válaszolható meg. A válaszhoz hozzátartozik, hogy meg tudjunk különböztetni egymástól egy komolyabb nehézséget és egy rutinérvelést. Elképzelhető, hogy egy matematikus, aki az algebrai számelmélet terén elismert szakembernek számít, képtelen megkülönböztetni a helyes és helytelen bizonyítást a nem standard analízis területén.
      Csak annyi biztos, hogy, mondjuk, az algebrai számelmélet képzett szakemberének tudnia kell: egy érvelésben melyek azok a kritikus pontok, ahova a szkepszisnek összpontosulnia kell; melyek egy érvben a „kényes” pontok, szemben a rutinszerűekkel; melyek azok a plauzibilisnek tűnő érvek, melyekről közismert, hogy hamisak.
      Egy matematikai kutatási beszámolót (illetve egy kézikönyvet vagy egy értekezést) soha nem teljes logikai részletességgel írnak meg. Ha ezt tennék, senki sem akarná, illetve senki nem is tudná elolvasni. Logikai szempontból való teljessége a szöveget semmivel sem tenné érthetőbbé; inkább érthetetlenebbé válna, kivéve talán a számítógépek számára. (A számítógép szempontjára alább még visszatérünk.)
      Ha nem a formállogikai értelemben vett teljesség, akkor mi biztosítja a matematikai bizonyítások helyességét a tényleges gyakorlatban? Nos, ott van(nak) például a bíráló(k), aki(k)nek a jóváhagyása szükséges feltétele a publikálásnak. Vajon e bírák az összes érv minden logikai részletét kiegészítik és ellenőrzik? Egyáltalán nem. Elvégre elfoglalt emberek, s az elbírálás a szakma szolgálatában ingyenesen történik, ráadásként az összes egyéb teendőik mellett. Nehéz lenne bármilyen világos képet alkotni a bírák tényleges működéséről, hiszen e tevékenység privát és félig anonim (a bíráló kilétét csak a szerkesztők ismerik). Biztos, hogy óriási a változatosság közöttük. Vannak olyanok, akik minden sort elolvasnak s minden számítást ellenőriznek; egyetlen olyan cikket sem hajlandók elbírálni, amely nem ellenőrizhető számukra ily módon. Az a benyomásunk, hogy a matematikai folyóiratokban publikált cikkeknek csak egy csekély százaléka részesül ilyen elbírálásban.
      Valaminek az efféle pontos ellenőrzésére csak egy másik olyan matematikus lenne hajlandó és képes, akinek az érdeklődése és képzettsége nagyon hasonló a szerzőéhez. Az ilyen bíráló valószínűleg pozitív előítéletekkel viszonyulna a hozzá benyújtott cikkhez, s így annak az egész matematikus közösséget érintő jelentőségéről, illetve fontosságáról nem feltétlenül nyújtana megbízható ítéletet. A szerző speciális érdeklődését kevésbé osztó kritikus talán objektívebbnek bizonyulna, ám feltehetően kevésbé alapos az olvasás tekintetében. Egy ismert amerikai matematikus, aki valószínűségszámítással foglalkozik, egy alkalommal a következőképpen jellemezte a bírálat folyamatát: „Megkeresed az érvelés leggyengébb részét, alaposan átvizsgálod, s ha az helyes, akkor úgy veszed, hogy valószínűleg az egész dolog rendben van.”
      Kétségtelen, hogy más tényezők is befolyásolják a bíráló ítéletét. „Illeszkednek-e”, indokoltnak tűnnek-e a módszerek és eredmények a bíráló az adott területről kialakított képének, általános kontextusának tükrében? Elfogadott, megbízhatónak ismert szerzőről van-e szó, vagy egy ismeretlenről, illetve – ami még rosszabb – egy olyanról, akiből közismerten hiányzik az eredetiség, és hajlamos hibázni?
      Mit jelent az, ha egy cikk megjelenik nyomtatásban? Erre nem lehet teljes biztonsággal válaszolni. Az is kérdéses, hogy megértette bárki is – a szerzőn kívül – a cikk tartalmát. Valamennyit segíthet, ha első kézből ismerjük az illető újság szerkesztői és bírálati elveit. Egy szerkesztő ezzel kapcsolatban így nyilatkozott: „Alkalmasan megválasztva a bírálót, bármely konkrét cikk számára biztosíthatom a pozitív vagy negatív megítélést.”
      Ha egy cikket egyszer publikáltak, úgy tűnhet, ki van téve az egész matematikus közösség alapos kritikájának. Ez távolról sincs így. A publikált matematikai cikkek többsége igen kevés olvasót vonz, s eltekintve a szerzőktől s talán a szerzők egyetemi tanítványaitól, néhány hónapon belül mindenki el is felejti őket.
      Persze vannak széles körben olvasott, befolyásos cikkek. A „széles körben olvasott”-at viszonylagosan kell érteni; a legtöbb matematikai szakterületen az aktív gyakorló tudósoknak (a kutatási beszámolók szerzőinek) a száma csak néhány száz fő. Egy befolyásos cikk eredményeit egy-kétszáz ember elolvassa, valamint bemutatják őket a szemináriumokon az egész országban s mindenütt a világon. Azokra a hallgatókra, illetve matematikusokra, akik egy ilyen cikkben komolyabb hibát képesek felfedezni, különdíj, jutalom vár. Ösztönző van arra is, hogy az olvasók a cikk eredményeihez kiterjesztéseket, általánosításokat, továbbá más eredményekkel való kapcsolatokat találjanak.
      Ha egy matematikai eredmény széles körű figyelmet vált ki és kiállja a folyamatos vizsgálat és elemzés próbáját, akkor bekerül a matematika megbízhatónak és ellenőrzöttnek mondható részébe.
      Garantált-e ez esetben annak bizonyossága? Természetesen nem. Eukleidész geometriája kétezer éven keresztül volt intenzív kutatás tárgya, mégis komoly logikai hiányosságokat tartalmazott, melyeket először csak az 1880-as években mutattak ki. Hogyan is lehetnénk valaha is biztosak abban, hogy nem vagyunk hasonlóan vakok érvelésünk valamely hiányosságával szemben?
      Márpedig – válaszolhatná valaki – igenis biztosak lehetünk benne! Pusztán vennünk kellene a fáradságot, akármilyen kellemetlen is, hogy matematikai bizonyításainkat (ügyelve arra, hogy azok csak olyan logikai lépésekből álljanak, amelyeknek feltételei beépíthetőek egy számítógépes programba) egy alkalmas programozási nyelvre átírjuk, s ily módon gépileg igazolhatóvá tegyük.
      Az ötletet tulajdonképpen már kipróbálták. A legkomolyabb ilyen irányú erőfeszítéseket a holland matematikus, N.G. de Bruijn és kollégái tették az 1970-es években. Kidolgoztak egy speciális számítógépes nyelvet, az AUTOMATH-ot s az ahhoz kapcsolódó Automath-programot. Céljuk az volt, hogy automatizálják a matematikai bizonyítások helyességének ellenőrzési folyamatát. A lázas kísérletezés évei után az Automath-programmal gyakorlatilag felhagytak. Mindez többféle módon magyarázható:

1. Egy rendes bizonyítási anyag formalizált megfelelőjét bonyolult leírni és nagyon hosszúra nyúlhat.

2. Még ha nagy mennyiségben rendelkezésre állnának is e fordítások az Automath-ra, hogyan lenne igazolható ezek helyessége, az, hogy maga az Automath-program helyes, hogy a gépi programot kifogástalanul írták meg, s hogy az hibátlanul futott?

3. A matematikusokat és informatikusokat nem igazán érdekli az efféle vállalkozás.

     Az Automath-megközelítés egy megvalósíthatatlan álmot jelent. A századfordulón még vélhették úgy, hogy bizonyításnak azt nevezzük, ami teljesen mechanikus módon igazolható. Ma, amikor sokkal átfogóbb mechanizációra van lehetőség, megfordult a dolog, és úgy hallani, a számítógépes feldolgozhatóság nem megkülönböztető ismérve a helyes bizonyításnak. Ugyanakkor a matematikus közösség által bevett gyakorlat alig változott, eltekintve attól, hogy munkájukban megnőtt a számítógép szerepe.
      E „formalizmus” nehézségeit elemi szinten megragadhatjuk, ha egy pillantást vetünk arra a kísérletre, mely egy nagyon egyszerű matematikai tétel teljes és szigorú bizonyítását kívánja megadni. Egy teljesen zárt, formális bizonyítás megadása a matematika mégoly apró problémájára is hihetetlenül bonyolult feladatnak bizonyul. Az állítólag szigorú bizonyítások rendszerint olyan hézagokat tartalmaznak, melyeket elfed az intuíció. Tekintsük az 1. táblázatban bemutatott példát. E táblázat – némi módosítással – egy kitűnő egyetemi tankönyvből származik. Ott arra szolgál, hogy az axiomatikus rendszerek működését szemléltesse, előkészítendő a nem euklideszi geometria kifejtését. Összevethető a magasabb szintű munkákban szereplő bizonyításokkal, mégis jóval kevésbé komplex, s az egyes lépések sokkal részletesebben ki vannak fejtve. Az 1. táblázat három, bizottságokra és azok tagjaira vonatkozó axiómát, továbbá egy tételt tartalmaz: „Mindenki legalább két bizottságnak tagja.” E tétel valóban következik az axiómákból. Mindez jól látható a 2. ábra diagramján. A példa célja azonban egy tökéletesen szigorú bizonyítás megadása. E szigorúnak tekintett bizonyítás tíz lépésben az 1. táblázat alsó felében található.
      Anélkül, hogy vitatnánk a konklúziót – miszerint az 1., 2. és 3. axiómából következik, hogy mindenki legalább két bizottság tagja – vizsgáljuk meg azt az állítást, hogy a „Bizonyítás” és „Q. E. D.” szimbólumok között elhelyezkedő írott anyag egy bizonyítást alkot. Az elfogadható bizonyításnak nincs formális definíciója. Az informális elképzelés szerint a bizonyítás egy egyértelmű és szigorúan formális nyelven leírt mondatoknak olyan sorozata, amely az axiómáktól a megengedett és formalizált logikai transzformációk segítségével a konklúzió felé halad.
      Átolvasva a bizonyítást, azt találjuk, hogy van egy lépés, melynek elfogadása a többinél nagyobb nehézséget jelent. A hetedik lépésről van szó. Ezen a ponton megállunk, s elménknek kemény munkára van szüksége, hogy továbbhaladhasson. Miért nem azonos C és E? Fejtsük ki az érveket egy kicsit részletesebben. Azért nem azonosak, mert r a (6.) sor szerint tagja E-nek, de az (5.) sor szerint nem tagja C-nek; így a bizottságok azonosságának definíciója értelmében C és E nem azonosak. E gondolatmenet megköveteli, hogy világosan szem előtt tartsunk három tényt, majd pedig mentálisan belássuk, hogy e helyzetből következik a nem-azonosság. Ezt a konklúziót abból a definícióból vezettük le, mely egyébként csak az azonosságról szól. Elménkben ezért, ezzel egyidejűleg, még néhány tényt fel kell idéznünk: mit jelent az azonosság, és hogyan kaphatjuk meg belőle a nem-azonosságot. Hogy világossá tegye, miről is van szó, a szerző fejtegetéseihez egy szimbolikus diagramot (2. ábra) mellékel, mely – állítása szerint – nem igazán része a bizonyításnak. A kép (amely nem része a „bizonyításnak”) biztosítja azt a meggyőződést és világosságot, melyet az „igazi bizonyítás” nem ért el kielégítő mértékben. Mindez egy meglehetősen különös helyzetet teremt számunkra: a bizonyítás nem meggyőző; ami ténylegesen meggyőz, az nem a bizonyítás.
      Az ember–ember vagy ember–gép érintkezésben mindig problémát jelent annak igazolása, hogy az, amiről valamit állítunk, tényleg olyan, mint amilyennek állítjuk. Például kijelentjük, hogy két egész számot helyesen adtunk össze, vagy hogy ilyen és ilyen adatokat megfelelő módon tápláltunk be a számítógépbe. Esetleg a számítógép arról tájékoztat bennünket, hogy helyesen hajtotta végre valamelyik eljárást. A közléstől az elfogadáshoz való átmenetnek végső soron logikán kívül eső kritériumok alapján kell megtörténnie.
      E problémával állandóan szembe kell néznünk. A fenti bizonyítás „érv”-oszlopában két rejtélyes szót találunk: az „elnevezés”-t és az „általánosítás”-t. Nincs kifejtve, hogy a bizonyításban milyen értelemben használták az „elnevezés” és az „általánosítás” terminusokat. Mármost, valóban, mindkettő bonyolult fogalom, s a filozófusok egész könyveket szenteltek ezek kifejtésére. Ha egyszer fontos szerepet játszanak a jelen kontextusban, hogyan igazoljuk, hogy az elnevezési vagy az átalakítási eljárást megfelelően hajtottuk végre?
      Tekintsük az „általánosítás” terminust! Az első lépésben kiválasztottunk és megneveztünk egy tetszőleges személyt. Lévén, hogy az illető egy tetszőleges személy, nincsen közelebbről meghatározva, hogy pontosan kiről is van szó. A gondolatmenet lényege, hogy ha valaki egy tetszőleges személlyel kapcsolatosan hoz fel érveket, s eközben kizárólag azon vonásokat veszi figyelembe, amelyek éppúgy megvannak az adott személyben, mint az összes többi emberben, akkor az illető levezetései az összes személyre érvényesek lesznek (10. sor). Nem kell-e akkor – a bizonyítás részeként – azt is igazolni, hogy csak az említett vonásokra támaszkodtunk a bizonyítás során? Mik a formális kritériumai ennek? Az efféle kérdések felvetésével a bizonyítást az igazolás mind mélyebb és mélyebb szintjei felé lehet kényszeríteni. Ami tehát most az érv-oszlopban áll – az a puszta szó, hogy „általánosítás” –, egyszerű retorika.
      Valamelyest különbözik az előbbitől a következő probléma. Tegyük fel, hogy felállítottunk néhány absztrakt axiómát. Honnan tudjuk, hogy létezik olyan rendszer, amelyik kielégíti ezeket az axiómákat? Ha nincs ilyen rendszer, akkor nem is igazán beszélünk semmiről. Ha van, akkor azt ismeretessé tehetné számunkra a következő megnyilatkozás: „Ilyen és ilyen definíciók mellett, így és így néz ki egy olyan rendszer, amelyik kielégíti az 1–3. axiómákat.” Vajon ez esetben egyszerűen rápillantanánk erre az állításra és elfogadnánk egy fejbólintással, avagy az megköveteli annak formális igazolását, hogy a rendszer állítólagos modellje valóban modell? Ezzel ismét az igazolás egy mélyebb szintjéhez jutottunk.
      Mindeme bonyodalmakra megoldást jelent, ha feladjuk a tökéletes szigorúság és teljes formalizáció felesleges és haszontalan célkitűzését. Ehelyett inkább elismerjük, hogy a matematika érvei egy emberi közönséghez szólnak, mely közönség rendelkezik azokkal a háttérismeretekkel, amelyek képessé teszik az előadó vagy a szerző intencióinak megértésére. Amikor a matematikai érvelésről azt állítottuk, hogy az nem mechanikus vagy nem formális, akkor implicit módon azt is elmondtuk, hogy ezzel szemben olyan közös jelentéseken alapuló emberi közlésforma, mely jelentéseknek nem mindegyike fogalmazható meg verbálisan vagy formális keretben.

Befejezés

     Következtetésünk az, hogy a teljesen formalizált és szigorú matematika mítosza valóban mítosz. A valóságban a matematika a társadalmi interakció egy formája, amelyben a „bizonyítás” a szabályszerűnek és a nem szabályszerűnek, a számításoknak és az alkalmi magyarázatoknak, a meggyőző érvelésnek, továbbá a fantáziának, az intuíciónak az elegye.
      A hozzáértő szakember tudja, hogy érvelésének melyek a sebezhető pontjai – melyek azok az részek, amelyekben a közönség várhatóan kételkedni fog. Ezek azok a részek, amelyeket gondosan részletez majd, ám a bizonyítás többi részét lerövidíti. Ezt azonban nem a szerző lustasága okozza, ellenkezőleg: a túlságosan részletező bizonyítás nehezebben emészthető, mint a túl rövid. A teljes matematikai bizonyítás nem azt jelenti, hogy számítógépprogramot írunk. A teljes bizonyítás egyszerűen kellőképpen részletes bizonyítást jelent – kellőképpen részleteset ahhoz, hogy meggyőzzük a megcélzott közönséget, a szakemberek egy olyan csoportját, amelynek tagjai a szerzővel összehasonlítható gondolkodásmóddal és képzettséggel rendelkeznek. Ebből következően az eredményeink helyességébe vetett bizalmunk nem abszolút, és természete sem különbözik alapvetően a mindennapi élet dolgaira vonatkozó ítéleteinkbe vetett bizalmunktól.

Novák Zsolt fordítása

Irodalom

Berlinsk, David 1976: On Systems Analysis. Cambridge, MIT Press.

Bruijn, N.G. de 1980: „A Survey of the Project Automath”. In J.P. Seldin – J.R. Hindley (szerk.): Essay on Combinatory Logic, Lambda Calculus, and Formalism. New York, Academic Press.

Davis, Philip J. – Hersh, Reuben 1981: The Mathematical Experience. Cambridge, Birkhäuser.

Koblitz, Neal 1981: „Mathematics as Propaganda”. In Arthur Steen Lynn (szerk.): Mathematics Tomorrow. New York, Springer-Verlag, 111–120. oldal.

Jegyzetek

1. Nehézkes felfogásúnak tartott törzs az ókori Görögországban. (A szerk.)

1. ábra

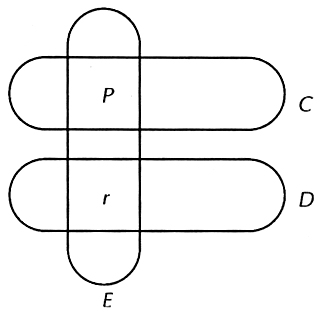
2. ábra: Bizottsági tagság

1. táblázat: Egyszerű példa egy deduktív rendszerre
A példa a szerző előzékenységének köszönhetően néhány változtatással Richard Y. Trudean The Non Euclidian Revolution (Cambridge, Birkhäuser Boston, 1987) című könyvéből származik.

Az alapfogalmak a „személy” és a „gyülekezet”.

Definíciók: „Bizottság”-nak nevezik egy vagy több személy gyülekezetét. A bizottságba tartozó személyt az illető bizottság „tagjának” nevezik. Két bizottság akkor azonos, ha az egyiknek minden tagja tagja a másiknak és megfordítva. Ha két bizottságnak nincsen közös tagja, akkor ezeket „diszjunkt” bizottságnak nevezik.

Axiómák:

1. Minden személy legalább egy bizottság tagja.
2. Bármely két személyre egy és csak egy olyan bizottság van, amelynek mindketten tagjai.
3. Minden bizottsághoz egy és csak egy diszjunkt bizottság található.

Tétel: Minden személy legalább két bizottság tagja.

Bizonyítás: