Perneczky Géza:

Képzômûvész
a matematika és a “szép arányok“ tartományai között

Amikor elôször kerestem fel a Saxon-Szász János - Dárdai Zsuzsa házaspárt, akiket elsôsorban mint az elektrografika képviselôit tartottam addig számon, azonnal kiderült, hogy Szász Jani nem csak az új, kísérleti mûfajok közé sorolható elektrografika jeles képviselôje, hanem “igazi festômûvész“ is, hiszen tele volt a lakása munkában lévô vagy már kész olajképekkel.

A legtöbb festmény majdnem monokróm volt, mert ezek csupán két szín, az erôteljes tónusú kadmium-sárga és világító erejû fehér mezôk kombinációiból épültek fel. De nem ez volt a különös, hanem az, hogy noha a képek elsô látásra nagyon is áttekinthetôen tagolt konstruktívista kompozícióknak tûntek, és a geometrikus absztrakció jól ismert stílusát követték – valahogyan mégsem voltak azok! Az egyszerûnek tûnô arányok mögött ugyanis szokatlan bonyolultság rejtôzött, és ez a nehezen kibogozható feszültség szinte bizsergetô volt. Aztán hirtelenül világos lett a számomra, hogy mit látok. – De hiszen ezek fraktálok! – kiáltottam fel. Tényleg azok voltak, és ez azért volt szenzáció, mert akkor már érdeklôdôként mintegy tíz esztendeje foglalkoztam a matematikának ezzel a viszonylag új ágával, ugyanakkor azonban mint mûvészettörténész, azt is megállapíthattam, hogy a fraktál-geometria alkotó jellegû képzômûvészeti alkalmazására mindaddig sehol sem találhattam sikeresnek mondható példát a világon.

A fraktál-geometria vizuális megjelenítése és szépsége ugyanis nem a mûvészet mûvelôinek a táborából érkezett, hanem a komputer-technika ajándéka volt, és a színes technika elterjedésével lepte meg az 1980-as években a világot. A mögöttük rejlô matematika is viszonylag újnak számított, de eredetileg csak a szakemberek szûkebb körét érdekelhette. Ekkor viszont a képernyôn megjelenô ábrák váratlanul igen színessé és gazdaggá váltak. Szinte pillanatok hódították meg a vizuális kultúra legkülönbözôbb tartományait, és olyannyira népszerûek lettek, hogy egyidôre még a vállalatok és nagybankok pazar kiállítású ajándék-naptárjainak az oldalairól is leszorították az impresszionista festmények reprodukcióit. Sokan voltak, akik csak azért vettek komputert, hogy a képernyôn megjeleníthessék, és esetleg ki is nyomtathassák például a Mandelbrot-halmazból kinagyítható szenzációs szépségû részleteket. A matematikában otthonosabbak pedig néhány új fraktál-képletre is rátalálhattak, és így “saját“ fraktál-geometriai képeket produkálhattak.

Ennél tovább azonban még a komputertechnika virtuózai vagy a vizuális kultúra ezermesterjei sem jutottak – a fraktál-képekbôl nem lett “mûvészet“, mert ezeknek a komputerrel generált érdekes alakzatoknak a matematikai háttere túl bonyolultnak bizonyult, és már csak a komputer-technikától való erôs függésük miatt is e képek megmaradtak bizonyos matematikai számítások elektronikus “kijelzéseinek“. Azóta elapadt a fraktálok körüli amatôr lelkesedés, és a fraktálgeometria (valamint a mögötte álló matematikai apparátus, a káosz-elmélet) visszatértek szûkebb szakterületükre, eredményeik pedig beépültek a különbözô tudományágakba. Saxon-Szász teljesítménye, hogy képzômûvészként is tudott valamit a fraktálokkal kezdeni, ezért tûnt szinte hihetetlennek.

Most, hogy közelebbrôl szeretnénk foglalkozni a munkáival, úgy érzem, hogy mindenekelôtt a fraktál-geometria miben létét kell – legalább is vázlatosan – az olvasó számára tisztázni.

*

Közmondásosan a régi görögökkel kell kezdenünk. A matematika kezdetei visszanyúlnak az ókori társadalmak szellemi és gazdasági életéig, így például a földek kimérésének a gyakorlata tette szükségessé a geometria kifejlôdését (a geometria szó maga is “föld-mérést“ jelent), jó példa erre Pythagorasz tétele, amely a derékszögû háromszögek oldalainak a nevezetes arányrendszerérôl szól. Valószínû, hogy a régi görögök az egyiptomiaktól vették át ezt az ismeretet, hiszen ott, ahol a Nilus áradási nyomán évente kellett újra kimérni a parcellákat, nagyon hamar megszülethetett az a felismerés, hogy egymást derékszögben metszô határvonalat úgy lehet a legegyszerûbben a földre rajzolni, ha kifeszített kötélbôl olyan háromszöget alkotunk, amelynek oldalai 3, 4, és 5 mértékegységbôl (vagy annak sokszorosából) állnak. Biztos, hogy az így rajzolt háromszög két befogója mindig 90 fokos szöget zár majd be – és ennek a gyakorlati ismeretnek a valamennyi derékszögû háromszögre általánosított formája az, amit ma Pythagorasz-tételnek nevezünk.

Egy másik jeles arányrendszer áttekinthetôbb természetû, de ennek az eredete is a korai görög filozófusok nevéhez fûzôdik. A “harmónia“ tanításáról van szó, a szép összhangok szabályairól. Ez az arányrendszer abból a felismerésbôl vette eredetét, hogy ha egy rezgô húrt a felénél lefogunk (az így létrejött arány 2 : 1), akkor egy nagyon szabályos hangközt, mégpedig pontosan egy oktávval magasabb hangot kapunk. A többi konszonáns (harmónikusan hangzó) hangköz is az egész számok arányai alapján képezhetô. A húrt ilyenkor 4 : 3, illetve 3 : 2 arányban kell osztanunk, aminek az eredményeképpen az így megszólaló (ahogy a görögök nevezték:) “szinfónikus“ hangközök a kvartnak és a kvintnek felelnek majd meg. Az ókorban egész kozmológiák születtek, amelyek a világmindenség felépítését a harmónikus arányokra osztott rezgô húr, és a rajta megszólaló “szinfónikus hangok“ törvényei alapján igyekeztek elképzelni – ez a felfogás tükrözôdik máig is a “szférák zenéje“ kifejezésben.

A bonyolultabb arányrendszerek legismertebb példája az aranymetszés, latinul az aurea sectio. Ilyenkor az “a“ rövidebb úgy aránylik a “b“ hosszabb szakaszhoz, mint a hosszabb szakasz a kettô összegéhez. Azaz ha “a“-nak nevezzük a rövidebbet, és “b“-nek a hosszabbat, akkor ez így írható le: a : b = b : (a + b). Az aranymetszésre, mint a legtökéletesebb és legszebb arányra az emberi kultúra egész történetén át találunk példákat, hiszen valamiképpen bele van építve a “szemmértékünkbe“ is, pontosabb megalkotására pedig már az ókortól kezdve geometriai szerkesztési módszereket használtak.

Az aranymetszéshez hasonló arányok számelméleti megközelitésére csak lényegesen késôbbrôl vannak adataink. Ezek egyike Fibonacci (eredeti nevén Leonardo Pisano) olasz matematikus a 13. században. A róla elnevezett Fibonacci sort úgy kapjuk meg, ha a számsor elejétôl elindulva olyan sort írunk fel, amelynek a következô tagját mindig a megelôzô két tag öszegébôl alkotjuk (1, 2, 3, 5, 8, 13, 21, 34, stb.). A számsor eleje még érdektelen, de ha ellenôrízzük, hogy elôrehaladtával a késôbbi tagok mennyire közelítik meg az aranymetszés követelményeit, akkor ahhoz a meglepô eredményhez jutunk, hogy már a hetedik és nyolcadik tag (vagyis a 21 és a 34) egymáshoz viszonyított arányánál is majdnem tökéletes az aranymetszésnek megfelelô aránypár, mert 21 : 34 – vagyis 0,6176 – már majdnem ugyanannyi, mint 34 : (34+21), azaz 0, 6181. A Fibonacci sor volt talán az elsô olyan matematikai objektum, amely felhívta az emberek figyelmét arra, hogy a progresszív ütemben elôrehaladó mûveletek nem szimpla ismétlések, hanem a mélyükön kreatív erôk rejtôznek.

A természet formái között igen gyakran találunk példát arra, hogy az aranymetszés aránya, vagy valamilyen más szembeötlô arány- és formarendszer egy-egy természeti produktumon belül ilyen progresszív módon ismétlôdik. A fák ágainak a rendje, a levelek erezetének a szélek felé elaprózódó hálója, vagy a páfrány csipkézettségének a páfránylevél oldalágain visszatérô kisebb léptékû megismétlôdése, de a csigaházak szerpentinvonalának a folyamatos tágulása vagy szûkülése is olyan rendszereket képez, amiknek az a fô jellegzetessége, hogy noha a részformák mérete bennük állandóan változik, e formák arányrendszere és jellegzetes alakja mégis annyira állandó marad, hogy ez a hasonlóság minden méretbeli különbséget áthidal. A másik megfigyelésünk pedig úgy szólhat, hogy felismerjük annak a fontosságát, hogy ezek az alakzatok és arányok (a Fibonacci sorhoz hasonlóan) szabályos sorba állíthatók, és a sor tagjai annyira szabályosan követik egymást, hogy akár végtelenbe veszô láncot is alkothatnak.

Úgy tûnik, hogy az élô és élettelen természet olyan dolgokat hoz létre, amelyeknek a részletformái egyazon tárgyon belül kisebb vagy nagyobb léptékben többszörösen is visszatérnek, más szóval: e részletformák alakja független a léptékváltástól. Mivel a dolgok ilyen jellegû változatlanságát (más szóval: “invariáns“ voltát) egyfajta tágabb értelemben vett szimmetriának is tekinthetjük (a tükrös szimmetriát felmutató tárgyak például invariánsak a részformák jobb- és baloldali elrendezettségével szemben), úgy is fogalmazhatnánk, hogy a természetnek, lám, meg van a maga geometriája vagy szimmetria-világa – a természeti formák legtöbbje invariáns a léptékváltással szemben.

Szembeötlô lehet, hogy bár az elmúlt évezredek emberi kultúrája már ismert olyan arányrendszereket – például az aranymetszést – ami lényegét tekintve olyan jellegû volt, hogy ez a nevezetes arány kisebb és nagyobb dimenziókban ismétlôdött meg a “szép“ tárgyakon (vagyis ez az arány már olyan sorozatot alkotott, amely elvben akár a végtelenségig is folytatható lett volna), mégis az elmúlt korszakok emberisége statikusan szemlélte a szimmetriának ezt a sajátos változatát, és nem épített fel lépcsôzetes sort, dinamikusan fejleszthetô, és matematikailag is leírható objektumokat az így kapott megfigyelésekbôl. Még a tudomány, vagy a mûvészetek területein sem alkotott az emberiség olyan dolgokat, amikben a szimmetriának ez a tulajdonképpen nagyon alapvetô formája, a léptékváltással szembeni invariáns jelleg a kérdés fontosságának a súlyával szerepelt volna. Csak a 20. században, és különösképpen a század utolsó harmadában, a komputer-technika kifejlôdésével jutottak el a matematikuson oda, hogy ennek a léptékváltással szenben invariáns sorok fontosságát teljes mélységében felismerhették. Ehhez egy a régi szemléletnél sokkal dinamikusabb világképre volt szükség – és természetesen az igen hosszú (elméletben végtelen) matematikai sorok számítástechnikai bonyolultságát is jól kezelni tudó komputertechnikára. Amikor aztán az egyes tudomány-ágak képviselôi el kezdték keresni a léptékváltással szemben invariánsan viselkedô formákat a saját szûkebb szakterületeiken is, kiderült, hogy szinte az egész természeti világ ilyen. Nem a régrôl ismert euklideszi geometria, hanem a szimmetriának ez a különös fajtája az, aminek alapján a világ megszervezôdik.

Az ennek a dinamikus szimmetriának megfelelô alakzatokat nevezte el aztán Benoît Mandelbrot fraktáloknak. Az elnevezés a latin “fractus“ melléknévi igenévbôl ered, ami “tört“-et jelent. Abból adódott, hogy az ilyen aránysorokra épülô formák karakterisztikus vonása, hogy a síkon kirajzolt körvonalaik vagy a térben megjelenô volumenük rajza nem hibátlanul két-, vagy három-dimenziós alakzat, hanem annál szabálytalanabb, elmosódott körvonalakra hajlamos, illetve “töredékes“, vagy “üreges“ formákat kiadó dolog – ahogy azt például a felhôk nehezen követhetô alakja, vagy a páfrány levelek sok türelmet igénylô többszörös csipkézettsége, illetve az emlôsállatok tüdejének a mikroszkópikus méretekig ismétlôdô elágazása is példázza. Mandelbrot matematikai felfedezései óta beszélhetünk például egy satírozássá sûrûsödô vonal esetében “másfél-dimenziós“ obejktumról, vagy ha egy térforma habfelületté válik, teszem azt “kettô egész nyolc tized dimenziós“ alakzatról.

*

Vessük össze az eddig mondottakat Saxon-Szász János képeivel.

A festmény, amelynek láttán felismertem, hogy tulajdonképpen fraktál-geometriai formákkal építkezik, a Dimenzió-lépcsôk címet viselte (a szónak abban az értelemben, amit a méretek változtatása, vagy a léptékváltás lépcsôzetessége kifejezés is jelenthet). Egy négyzet volt ennek a kompozíciónak a kiinduló pontja, amelyet Saxon úgy osztott kisebb részekre, hogy az egyik oldalát, mégpedig a négyzet jobb-oldali élét, három részre osztotta. Ezután pedig kiemelte az itt megrajzolható három kisebb négyzet közül a középsôt, majd egy lépéssel tovább ment, és megismételte ezt a mûveletet azzal az újabb négyzettel, amit a hiányzó középsô négyzet belsô éle mellé rajzolhatott. Innen aztán újra tovább lehet lépni egy még kisebb négyzet felé, és a munka elvben a végtelenségig folytatható. (Íme, itt a léptékváltással szemben mutatkozó invariáns jelleg!)

Ezen a lépcsôn temészetesen nehéz lenne messzire haladni, mert már az elsô néhány lépés után annyira apró formák állnának elô, hogy körülményes lenne a további harmadolást egy táblaképen belül nem csak elgondolni, hanem tényleg meg is festeni. Saxon-Szász is megelégedett azzal, hogy a kiindulópontul szolgáló négyzeten (egyre kisebb léptékben) háromszor végezze el ezt az osztást, azután megállt. A festmény létrejöttének a logikai lépéseit az alábbi vázlatrajz mutatja:

A kortárs mûvészetben jártas olvasó a kész festményt tulajdonképpen odasorolhatná a “shaped cancas“ (formára vágott, formázott) mûfajhoz tartozó geometrikus kompozíciók közé is (mert a képtáblából a hiányzó jobboldali négyzetformák ténylegesen ki vannak vágva, azaz a kép széle fizikailag is “formázva“ van). Ám a kép egyik szembeötlô jellegzetessége ezen túl még valami plusszal is szolgál. Ez a többlet pedig az a dinamika, amely a nézôt szinte felszólítja arra, hogy gondolatban tovább folytassa a festmény középen elôálló, és egyre kisebb méretû négyzetek elôállítását egészen a végtelenségig. Belátható, hogy ha ezt tennénk, akkor a képnek ez a “csorba“ éle egyre sûrûbb csipkézettségû lenne, és végül oda jutnánk, hogy már nem tudnánk pontosan meghatározni az így elôállt, és egyre töredezettebb határvonal hosszát sem – illetve azt kellene mondanunk, hogy ez a hossz végtelen, mert a kész határvonal legbelsô pontjához még mindig hozzá fûzhetnénk a következô lépésben egy újabb, még kisebb léptékû öbölszerû függeléket, és ennek a kiegészítésnek elvben soha nem lenne vége.

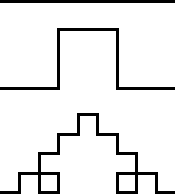
Az így kapott határvonal pedig már sok szempontból megfelel a fraktálokkal szemben támasztott követelménynek is, hiszen semmi másból nem áll, mint annak a szemléltetésébôl, hogy a kiinduló alapforma az objuktumon belül újra-és-újra elôfordul, mégpedig egyre kisebb léptékben. A kész rajzolat tulajdonképpen nem más, mint egyetlen, alapvetô formának a léptékváltástól független ismétlése. Mint érdekességet említem csak meg, hogy ha Saxon a négyzet jobboldalába belehasító töredezett él valamennyi szakaszán is elvégezné ezt az egyre apróbb formákra bomló osztást, akkor a fraktál-geometria egyik klasszikus esetének, a Koch-görbének egy változatához jutna el. Íme ennek a lehetséges osztásnak az elsô három lépése a Koch görbénél és a “Saxon-görbénél“:

Koch-görbe	Saxon-görbe

Még egy érdekes ismerettel toldanám meg ezt a példát. Mandelbrot, a fraktál-geomeria legismertebb kutatója éppen a töredezettségnek azt a mértékét nevezte meg a fraktálok jellegzetes paraméterének, vagyis ez az az adat, amit – ahogy errôl már fentebb is szó volt – tört számokkal kifejezhetô dimenziókkal adhatunk vissza. Mandelbrot definíciója szerint a “fraktál-dimenzió“ nagyságát úgy kapjuk meg, ha egy olyan tört logaritmusát keressük, aminek a számlálójában a töredezettséghez elérésére használt lépések száma, nevezôjében pedig az eközben elôállt tényleges méret nagysága szerepel. A Koch-görbénél négy vonal-szakasznyi lépéssel is csak három szakasznyi lett a kész görbe hossza (ez leolvasható a fenti ábráról is), vagyis a görbe fraktál-dimenziója 4/3-nak a logarimusa lesz, ez pedig 1,2618... Ha ugyanezt a számítást a “Saxon-görbénél“ végezzük el, akkor pedig abból kell kiindulnunk, hogy ott meg öt tényleges vonal-szakasznyi lépéssel értünk el három szakasz volumenû formát, vagyis a keresett fraktál-dimenzió az 5/3-nak lesz a logaritmusa, ez pedig 1,4649...

Ha ezt a két eredményt összehasonlítjuk, akkor azt is megfigyelhetjük, hogy a Koch- görbe “rezgése“, töredezettsége, noha már maga mögött hagyta az egy-dimenziós vonalak szimpla világát, még mindig közelebb áll a vonalhoz, mint a “Saxon-görbe“ majdnem másfél dimenziós csipkézettsége, vagyis a “Saxon-görbe" jobban közelít a két-dimenziós sík-idomok felé (azaz erôsebben “satíroz“).

Mivel a tört számokkal jelölt fraktál-diemenziók tulajdonképpen csak akkor válnának fizikailag is valóságos dolgokká, ha a fraktálformák töredezettségét elállító mûveleteket, az osztást vagy a felaprózást tényleg a végtelenségig tudnánk folytatni, ideális esetben minden egyes fraktál-forma végtelen méreteket venne fel, töredékes, “porózus“ szerkezetével mind a mikroszkópikus, mind pedig a makroszkópikus irányba haladva akkorára nône, hogy minden más formát kiszorítana a világmindenségbôl. Ez a gondolati aktus természetesen jellegzetesen emberi általánosítás, és a természetben más a helyzet, hiszen a fraktálalakzatoknak határt szabnak az anyagi világ törvényei. Ott jól megfér egymás mellett, vagy egymáson áthatolva az a néhány millió fraktál, amit például bármelyik légifelvétel is mutat a földfelszín valamelyik kis darabjáról (Ezt az egymásba rajzolt fraktál-geometriai szerkezetet “szabad szemmel“ persze nem látjuk, de M. F. Barnsley amerikai matematikus mégis kidolgozta azt a módszert, amellyel a fantasztikus részletgazdagságú szatelit-felvételeket – a könyebb tárolás céljából – néhány ezer fraktál képletére lehet tömöríteni).

Hogy a roppant esetlegesnek tûnô légifelvételek is felbonthatók fraktálokra, vagyis abszolút szabályossá tett, és ezen az úton matematikailag mérhetô alakzatokra, az azt mutatja, hogy a könyvek lapjain látható megkapó szépségû fraktálrajzok (és ugyanígy a velük rokon Saxon-Szász munkák is) igencsak “megtisztított“ és idealizált formák már, és e tekintetben nem különböznek az analitikus gondolkodás által létrehozott többi emberi fogalomtól vagy kultúrális produktumtól, például az euklideszi geometria szintén ideálisan tiszta alakzataitól. Ez a felismerés nem csak ismeretelméletileg fontos, hanem – ahogy azt késôbb látni fogjuk – az esztétikai megítélés szempontjából is jelentôs lehet.

Hogy Saxon-Szász munkáinak a jelentôségét megértsük, térjünk vissza még egy pillanatra a fraktál-formák történelmi múltjához. Amint már említettem, meglepô, hogy bár a természet tele van fraktál-jellegû formákkal, az emberi kultúra múltjában mégis hiába keresnénk ilyen alakzatokat. Az ember, úgy látszik az euklideszi geometria nagyon áttekinthetô és egyszerû formáiban tanult meg gondolkodni. Úgy tûnik, hogy a nagyon kevés fraktál-rajzolat közül, amit emberi kéz (véletlenül?) alkotott, az olaszországi Anagni város 12. században épült katedrálisának a mozaik-dísze a legrégibb. Az itt látható díszítô ábrák ugyanis olyan ornamentális elemekbôl épülnek fel, amik tulajdonképpen hibátlan fraktálok, és amilyenhez hasonló formákat elôször csak sokkal késôbb, 1915-ben alkotott Sierpinski, lengyel matematikus.

Mozaik-dísz, Anagni, katedrális	Sierpienski háromszög

Mandelbrot, aki szeretett a matematika múltjában kutatásokat is végezni, és ezért könyvtárnyi reprodukciós kötetet lapozott át a mûvészettörténet területérôl is, minden igyekezete ellenére is csak igen kevés kultúrális eredetû fraktál jellegû képre lelt. Például Leonardo da Vinci vízözönt ábrázoló rajzainak, vagy Hokusai híres “Nagy hullám“ címû fametszetének a láttán vélte úgy, hogy ezek fraktál-alakzatokhoz hasonló, a részletformákat kisebb-nagyobb léptékben ismétlô rajzolatokat tartalmaznak. De a matematikusok is elôször csak a 19. században jutottak el a fraktálokhoz hasonló matematikai objektumok közelébe.

Hausdorff német és Poincaré francia matematikusok olyan matematikai sorokkal foglalkoztak, amikrôl ma már tudjuk, hogy végtelen töredezettségük vagy bonyolultságuk révén az un. nem-lineáris matematika tartományaiba sorolhatók, és grafikai megjelenítésük fraktálokat eredményez. Poincaré azonban ezeket a nehezen kezelhetô leleményeket még “monsztereknek“, matematikai szörnyszülötteknek nevezte, mert sem az euklideszi geometria alapján, sem pedig az addig ismert matemaikai módszerekkel (például a differenciál- és integrál-számítás segítségével) nem voltak egykönnyen kezelhetôk. Az ô nyomdokaikon haladva azonban – s különösen az 1900-as századforduló körüli években – már többen akadtak, akik hasonló “szörnyekre“ bukkantak, és egymás után alkották meg azokat a matematikai és geometriai objektumokat, amiket ma már a fraktálok világához sorolunk (ilyenek voltak Georg Cantor, H. von Koch, Waclaw Sierpinski, illetve Giuseppe Peano és Gaston Julia is).

De csak Mandelbrot volt az, aki az 1970-es években szakított azzal a felfogással, hogy ezek a formációk tényleg obskurus, szörnyszülött dolgok lennének. Neki ugyanis sikerült olyan technikát kidolgoznia, amivel ezek a végtelenségig felaprózódó (majdnem hogy porrá szétesô) formák kezelhetôk lettek, és paramétereik is mérhetôvé váltak. És ô döbbent rá elôször arra is, hogy a természet építkezési logikája éppen a léptékváltással szemben invariáns tulajdonságokat mutató formavilágon, a fraktál-geometrián nyugszik. Az 1970-as évek végén és a 80-asok elején jelentette meg az e tárgykörben írt legfontosabb publikációit, de Magyarországon elôször csak egy jó évtizeddel késôbb, és akkor is csak igen szórványosan váltak hozzáférhetôvé a matematika eme új fejezetét tárgyaló közlemények.

*

Annál érdekesebb viszont, hogy ezektôl az eseményektôl teljesen függetlenül Saxon-Szász János, aki a hetvenes évek végén még nyíregyházi gimnazista volt, már elsô papírra vetett munkájában is a szimmetria-váltás különös eseteivel és a lépték-változtatás ábrázolásának a lehetôségeivel foglalkozott. Ennek dokumentuma például az az 1979-es datálású Univerzum címû grafika, amit Csiky Tibor és Fajó János vezette gönci nyári alkotótábor résztvevôjeként készített tizenöt éves korában.

Saxon-Szász János: Univerzum (1979)

A gönczi, majd encsi konstruktívista szellemû szabadiskolának a következô évek alatt is látogatója maradt, majd 1982-tôl, amikor Budapestre költözött, a Pesti Mûhely körében dolgozott tovább, és ez idô alatt készült grafikái, szobrai, festményei javarészt szintén konstruktívista szellemben készültek.

Megpróbált az Iparmûvészeti Fôiskolára is felvételt nyerni, de mivel ez nem sikerült, a Bánki Donát Mûszaki Fôiskola hallgatója lett, mégpedig azzal a megfontolással, hogy az ott szerzett technológiai ismereteket hasznosítani tudja a fémszobrászatban is. Az 1988-ban készült Struktúra címû olaj/vászon kompozíció pedig azt igazolja, hogy az ez idôben készült konstruktivista munkái kapcsán is még mindig a lépték-váltó formák érdekelték ôt.

A kilencvenes években az Arden Quin vezette, MADI nevû nemzetközi konstruktívista mûvész-mozgalom tagja lett (az elnevezés a Mozgás, Absztrakció, Dimezió, Invenció rövidítésébôl adódott), és az itt uralkodó szabad szellem és kísérletezô kedv hozzásegítették ôt ahhoz, hogy például felismerje, hogy milyen lehetôségek rejlenek abban, ha a festmények elhagyják a négyszögletes táblakép formáját és az objekt alkotás különbözô módozataival éljenek – végeredményben ezen az úton jutott el a “shaped canvas“ mûvek, a “formázott“ festmények mûfajáig.

Lehet, hogy Saxon-Szász matematikusként valahonnan Poincarétól elindulva újra felfedezte volna azt, amit pár esztendôvel korábban Mandelbrot éppen megalkotott. A mûszaki fôiskola bejezése után hozott döntései és a különbözô mûvészi körökhöz vagy iskolákhoz való csatlakozása nyomán viszont az történt, hogy képzômûvész hajlamai és vele született matematikai készségei együttesen ahhoz segítették ôt hozzá, hogy ne a matematika sterilebb szintjén, hanem a mûvészetben már nagy tradícióval rendelkezô geometriai absztrakció nyelvén dolgozza ki a munkássága alapjául szolgáló (és végeredményben a fraktál-geometriával rokon) forma-rendszert és alkotásmódot.

Saxon-Szász János: Struktúra (1988)

Csak természetes, hogy ennek kapcsán olyan terminológiát használt, ami független maradt a matematikai kutatások nemzetközi mezônyétôl, és inkább kapcsolódott például a konstruktivizmus nyelvéhez. A különbségeket tekintve az a legfontosabb és legjellemzôbb, hogy Saxon-Szász a dimenzió szót következetesen a “nagyságrend“, illetve a “lépték“ értelmében használja, és nem pedig úgy, ahogy a szót a két-dimenziós sík, vagy három-dimenzós tér említésekor használjuk. Ha tehát polidimenziós mezôkrôl beszél, akkor az ilyen mezôket olyan munkaterületként kell érteni, ahol kisebb és nagyobb dimenziókban ismétlôdnek meg a formák, és ezért minden motívum alá van rendelve az egész mûalkotáson átvonuló lépték-váltás (dimenzió-váltás) lépcsôzetes ritmusának (és nem pedig arra kell gondolnunk, hogy itt esetleg négy- vagy öt-dimenziós science-fiction tárgyakról lenne szó).

Magát a léptékváltást, illetve az azt lehetôvé tevô ismétlési logikát a matematika a mûveletek megismétlésére utaló “iteráció“ szóval jelöli (innen az “iterált matematika/geometria“ kifejezés is). Saxon-Szász a kilencvenes évek elejétôl kezdve már egymásután alkotta meg azokat a képeit, amik nem próbálkozások vagy spekulatív kutatómunkák többé, hanem amiknek a láttán bármely matematikus is azonnal iterált geometriáról vagy fraktálokról beszélne – noha az is biztos, hogy Saxon-Szász ugyanezen mûveit meg egy mûkritikus elsôsorban mégis csak a képzômûvészet produktumaihoz sorolná, s legfeljebb azt tenné ehhez hozzá, hogy a fraktál-geometria e képeken ideogrammákká alakul át, azaz jelképes szerepbe állítva tér vissza. Saxon-Szásznak sikerült a két egymástól nagyon messze fekvô tartományt, a matematikát és a képzômûvészeti közlésvilágot tökéletesen összebékíteni.

Munkáira a kilencvenes években már több nemzetközi fórum is felfigyelt, kiállítási lehetôségeket és ösztöndíjakat kapott. Különösen fontosnak bizonyult a dél-francia-országi Mouans-Santoux-i Espace de l’Art Concrete központ meghívása. Itt ugyanis nem csak öt hónapos mûtermi munkára nyílt lehetôsége, hanem az is a felaladatai közé tartozott, hogy egy alkotókört vezessen, ahol meg is kellett fogalmaznia az elképzeléseit. Ennek az ösztöndíjnak és az ott végzett munkának a kapcsán született meg az Espace l’Art Concrete és a MADI támogatásával a Dimenzió ceruza (Dimension Crayon) címû többnyelvû kiadvány, amelyben Saxon-Szász Poly Universum címen összefoglalta programját – és ez a szöveg egyszerre nevezhetô mûvészeti káltványnak és a fraktál-geometria egy sajátos változatát definiáló proklamációnak.

Az a körülmény, hogy Saxon-Szász itt azonnal univerzumról beszél, két igen fontos, és a mûvész egész munkásságára jellemzô dologra vet fényt. Az egyik magából a fraktál-geometriából eredeztethetô, hiszen a végtelen sorokkal folytatot munka logikájából következik. Ha ugyanis az iterált geometria elvben a végtelenségig kiszámítandó sorokkal dolgozik, akkor – ahogy errôl már volt szó – minden egyes modell, legalább is elvben, végtelen kiterjedésû. És ez az elvi maximalizmus valóban azt a benyomást keltheti, hogy egy-egy ilyen fraktál – legalább is gondolatban – önálló világ, olyan kész univerzum, amelyben kizárólagos érvényû törvények dolgoznak.

Saxon-Szász János: A „Dimension crayon” c. kiadvány címlapja

A másik jellegzetesség pedig ennek a messzemenôen idealizált állapotnak a következménye. Ha ugyanis egy-egy modell (a mi esetünkben: képzômûvészeti mû) a saját logikai rendszerén belül egy-egy lehetséges világ jelzésszerû ábrázolásának tekinthetô, és olyan, mint egy elgondolt univer-zum, akkor az így megalkotott modellek (vagy mûvészi alkotások) már utópiák, mégpedig úgy, ahogy a szót Morus Tamás is használta: jelképes értelmû szigetek, amelyek szemben állnak a való világgal, mint annak lehetséges alternatívái, “jobb“ változatai.

Saxon-Szász oeuvre-jében van egy mû, mégpedig az eddigi legkomplexebb alkotása, a Polidimenzionális sakk, amelyik kitûnôen szemlélteti ezt az utópisztikus sziget-funkciót. Ez a háromdimenziós objektum olyan sakktáblát modellez, amelyiknek a mezôi a tábla középpontjától kifelé haladva egy konstans léptékváltozás arányában lépésrôl-lépésre kissebbek lesznek. Ez természetesen azt jelenti, hogy ebben az univerzumban minden lépés együtt jár a figurák méretváltozásával is. Sôt, ha elfogadjuk e táblát, mint univerzális érvényû modellt, akkor a léptékváltás ritmusa a figurákon túl még egy sor egyéb dologra érvényessé kell hogy váljon, így például kötelezô erejû lesz mindazon tárgyakra vagy személyekre, akik a táblával kapcsolatba kerültek – adott esetben tehát a sakktáblához leülô játékosokra is. A sakktábla köré így végül is odaférhet akár az egész világ, miközben ez a külön

Saxon-Szász János: Dimnezió sakk

univerzum úgy tágul a maga belsô törvényei szerint határtalanná, hogy a kivülálló számára néhány centiméterre a tábla szélétôl már láthatatlanul kicsinnyé zsugorodik.

Vonjuk le ebbôl a tanulságot: Saxon-Szász az univerzum szó használatával a mellett tette le a garast, hogy a képeit tényleg lehetséges világoknak, univerzális érvényû modelleknek tekinti, és ezzel a lépésével az avantgárd utópiák hosszú sorához csatlakozott. Csak emlékeztetni akarok itt Málevics munkásságának kiindulópontjára, a Fekete négyzet-re, amit Málevics egy lehetséges új kozmosz modelljének szánt, és megemlíteném szuprematista kiáltványait, amelyekben az ehhez hasonló formák rendszere ténylegesen is mint világmodell szerepel. Felhivnám továbbá a figyelmet arra a körülményre is, hogy ennek megfelelôen Málevics nem csak grafikákat és képeket, hanem térbeli formákat, szuprematista architektúrákat is alkotott – mintha csakugyan újra akarta volna teremteni velük a világot. Hasonlóan univerzális igényekkel lépett fel a konstruktívizmuson belül Mondrian is a maga jellegzetes szerkezetû festményeivel. Le Corbusier pedig egyenesen odáig ment el, hogy egész városokat (de legszívesebben országokat, vagy egy újabb Földgyolyót) tervezett volna meg a maga utópisztikus ízû modellje alapján, amelyet – és ez roppant érdekes! – ô is ellátott egy alapvetô arányrendszerrel, mégpedig az aranymetszést és ez emberi arányokat egyaránt figyelembe vevô un. “modulor“-ral.

Az pedig már csak hab a tortán, hogy a fraktál-geometria bonyolultabb formáival foglalkozva, az úgynevezett periódus-duplázással operáló fraktálok kutatása során egy szintén modell-értékû “modulor“-ra, konstans számra bukkantak a kutatók. Ez az állandót, az úgynevezett Feigenbaum-számot (Mitchell Feigenbaum, pszi=4,669201...), amelynek a fontossága csak a pi-hez hasonlítható, univerzális állandónak nevezték el a matematikusok, mert az egész világegyetemre érvényes módon adja meg a komplexebb felépítésû objektumok, események, struktúrák és arányok kulcs-számát, magyarán annak az arány-küszöbnek a számsorba elfoglalt helyét, ahol a léptékváltást meghatározó kritikus változás vagy ugrás történik. (Hogy a hatványozást és a rekurzív számolási technikát egyaránt használó komplex sorok és fraktálok, pl. a Mandelbrot-halmaz esetében a lépték-váltás tényleg csak a fenti “pszi“ szám arányában lehetséges, és hogy ennek a számnak a szerepe ugyanúgy kényszerítô erejû, mint a kör és a rádiusza viszonyának az esetében a pi, az matematikailag igazolható.)

Noha a Feigenbaum-szám csak a fizikai világban mûködik, mégis azt mondhatnánk, hogy a vele kapcsolatos emberi reakciók és a belôle levonható következtetések néha annyira fantasztikusak, hogy ilyenkor ezek a spekulációk nem is annyira tudományos elméleteknek, mint inkább az általános emberi kultúra részeinek tûnhetnek. És fordítva is megfigyelhetô a határok elmosódása: Saxon-Szász munkái a képzômûvészet birodalmához tartoznak, de mégis úgy vannak megalkotva, hogy kompozíciójukban természettudományos szigorral megalkotott arány-számok, “modulorok“, játszanak fontos szerepet. Hogy mindezek ellenére Saxon-Szász mégis képzômûvész maradt, az azzal magyarázható, hogy mûveinek funkciója mégis csak kultúrális jellegû. Részletmegoldásaiban is sok, csak is a festészet tradícióiból levezethetô elem fedezhetô fel.

Az egyik legérdekesebb formai elem, ami által polidimenzionális kompozíciói a fraktálokhoz való minden hasonlóságuk ellenére sem válnak azok egyszerû illusztrációivá, a képek felépítésében szereplô “segédsíkok“. Ezek úgy jöhetnek létre, hogy egy-egy forma geometrikus iterálásával, és az

Példa a „háttérben” mgjelenô segédsíkokra (szürke mezôk)

így született alakzatok elrendezésével Saxon-Szász a mûalkotást még nem tekinti feltétlenül késznek, hanem él azzal a lehetôséggel is, hogy a sarokpontokat összekötve és a hézagokat áthidalva “hátteret“ adjon a kompozíciónak. Ez a procedúra a matematika oldaláról nézve önkényes lépés, a festmények kulturális hátterét tekintve azonban fontos esztétikai plusz, mert ezzel válik a mû jelképes erejû táblaképpé, ikonná, és kapja meg azt a szimbólumokban gazdag aurát, ami közel hozza a mûvet a szakrális funkciókhoz is. Saxon-Szász esetében az utópisztikus mondanivaló ez a kvázi-szakrális elem – annak a szándéknak a hangsúlyozása, hogy ezek a mûvek normákat, törvényeket definiálnak, és egy-egy lehetséges világ jelképes modelljei. Megint csak Málevics nevét és a szuprematista képek ikonszerû felépítését kell, mint analóg példát említenem.

Saxon-Szász János: Polidimenzionális fekete négyzet

Csak ritkán fordul az elô, hogy egy-egy iterálható geometrikus forma önmagában, is alkalmas legyen az ikon szerepre. Ha mégis ilyenre bukkanunk, akkor a táblaképhez fûzôdô formai rokonságával magyarázható. Például a négyzet számíthat ilyennek, mert tábla alakú. Saxon-Szász egy esetben tényleg Málevics Fekete négyzetét választotta kiinduló pontul, és ennek a mûnek Polidimenzionális fekete négyzet címet adta. Oldalait 1 : 5 arányban osztotta fel, és ezzel a léptékváltással alkotta meg a formát körülölelô “rojtokat“. Az osztást a képen háromszor végezte el. Az így kapott csipkézett forma körvonala rokon azokkal a belsô határvonalakkal, amiket a korábban már említett Dimenzió lépcsôk címû képbôl olvashattunk ki.

(Csak zárójelben: Ez esetben is kiszámítható a körvonalak fraktál-dimenziója. A jelen esetben 11 szakasszal értünk el 5 szakasznyi méretváltozást, ezért log 11/5 keresve kapjuk meg az eredményt, ami 1,4898...)

A mûvek közt tallózva egy egész sor olyan kompozíciót találunk még, ahol nem egy, hanem legalább két geometrikus alakzat iterálása hozta létre a kész mûveket. Leggyakrabban szögletes formák és körívek szerepelnek egymásba ágyazva e képeken, mert ezek így együtt élesebb kontrasztot adnak és vizuálisan is gazdagítják a kompozíciót. Saxon-Szász az ilyen több alapelembôl álló kompozíciós sémákat, szemben az egyetlen alakzatból komponált alkotásokkal, amik “tiszta formák“, “kevert formák“-nak nevezi.

A matematika is ismeri az ehhez hasonló összetettebb iterálást. Saxon-Szász azonban nem ezeket a matematikai elôképeket követte, hanem csak a természeti világhoz lépett közelebb a maga alkotta “kevert formáival“, mert – ahogy már említettem – bár igaz az, hogy a környezetünk formavilága igen nagyszámú fraktálra bontható fel, mégis az a helyzet, hogy ezek között tényleg csak igen ritkán fordulnak elô a fraktál-képeskönyvekbe is beleillô “tiszta formák“ vagy “uni-fraktálok“. A valóságos világban található alakzatoknak a kódjában sok a “random“ – vagyis a véletlen szerepét is a kódba író – elem. Azon kívül számos természeti forma esetében, ha megpróbáljuk fraktálokra visszavezetni ôket, az bizonyosodik be, hogy felépítésük logikája többszörös kóddal, több egymásba fonódó arány-rendszerekkel fejthetô csak meg.

Mindahhoz, amit eddig elmondtunk, kiegészítésként hozzáfûzhetünk még annyit, hogy Saxon-Szász idônként olyan munkákat is készít, amelyek matematikai háttere nem sorolható a fraktálgeometriához, de ezek a mûvek is az arányokkal való játék szülöttei. Ilyenek például azok a forma-szekvenciák, amelyek megôrzik a kiindulásként vett alakzat volumenét, de lépésrôl-lépésre megváltoztatják a szélesség és a hosszúság egymáshoz mért arányát. Ilyenkor elôfordulhat az, hogy egy-egy kompozíció nyúlni kezd, mintha csak a kozmológiából ismert "fekete lyuk" szívó hatásának engedne, és az a veszély fenyegetné ôt, hogy átmegy a "szingularitásba", ahol minden tárgy a cérnaszálnál is vékonyabb, de nagyon hosszú fonallá nyúlik. Noha az ilyen kompozíciók magasba nyúló alakjukkal nehezen férnek el egy, a jelen kiadványhoz hasonló füzet lapjain, mégis ezekbôl a mûvekbôl is hoztunk a képanyagban mutatót, annál is inkább, mert valószínû, hogy a mûvész a jövôben is engedni fog a kísértésnek, hogy az arányokkal való kreatív játék legkülönbözôbb irányú lehetôségeivel foglalkozzon.

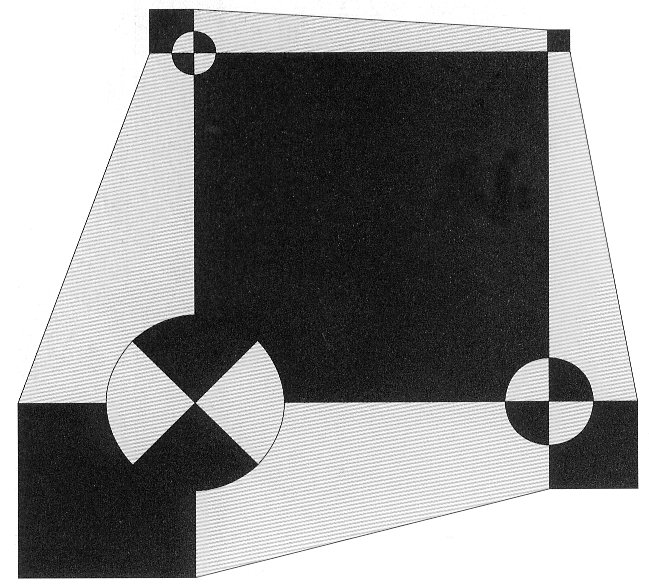
Példa a „’kevert formákra”: Saxon-Szász János: Mozgás

Ennyit a fraktál-geometria és Saxon-Szász mûvészetének a közvetlen kapcsolatairól. Mindezek a példák azonban megmaradnak a mesterség szakmai kérdéseinél, és nem lépnek túl azon, hogy mûvek matematikai hátterérôl is szóljanak. Saxon-Szász mûvészete azonban a képzômûvészeten belül maradó kultúrális teljesítmény, és bár az eddig elmondottak megértése szükséges ahhoz, hogy ezt a mûvészetet a helyére tegyük, ennek a helynek a pontosabb meghatározására mégis csak képzômûvésze tágabb birodalamának a figyelembevételével lehetséges.

*

Többször szóba került már a konstruktívista tradíciók fontossága, hiszen Saxon-Szász tevékenysége végül is a 20. század mûvészetének ehhez a fejezetéhez kapcsolódik. Kérdés azonban, hogy ez a majdnem száz esztendôs tradíció mennyiben tekinthetô élô hagyománynak még, és ha van még aktualitása, milyen érvényel képes az ô igen egyéni teljesítményét magába fogadni?

A konstruktívizmus egy közel évszázados történetét több fejezetre oszthatjuk, de ezekben a periódusokban tulajdonképpen csak két egymásnak nagyon is ellentmondó törekvés jutott vezetô szerephez váltakozó erôvel.

Az egyik domináló törekvés kifejezetten morális tartalmú és ideológiai természetû volt, mégpedig egy normatív, majdnem hogy vallásosan messianisztikus program hangsúlyozása. Ez tagadta a világ látható formáinak a fontosságát, és arra összpontosította a figyelmét, hogy a természeti formák mögött rejlô szellemi világot juttassa szóhoz. Ennek megfelelôen egyszerû formákká redukált jelképeket, ikonszerû szimbólumokat helyezett a mûvészet középpontjába, és ezek segítségével igyekezett az erkölcsi és szellemi értékeket szolgálni. Már a kezdeteknél, Málevics mûvészetében is ez az ideológiai tartalom került túlsúlyba, olyannyira, hogy a szuprematista mûvek geometrikusan tagolt, “technicista“ formavilága csak másodlagos fontosságúnak tûnhetett. (Ezek a geometrikus formák tényleg nem a technika világából, hanem az orosz népmûvészet ornamentikájából, valamint a pravoszáv ikonfestészet sík-geometriai formákra redukáló nyelvébôl vették az eredetüket).

A másik vonulat a gyakorlati élet nyújtotta feladatok fontosságát hangsúlyozta és a geometriára leegyszerûsített mûvészetet is ennek a feladatnak a szolgálatába igyekezett állítani. Ezt a felfogást legtisztábban a Bauhaus programjából ismerjük (képviselôik: Gropius, Moholy-Nagy, Bauer Marcell, stb.). De az orosz konstruktívisták táborán belül is volt egy csoport, amely a forma-tervezést és a gyakorlati életben felmerülô felaldatok megoldását tekintette feladatául (említsük meg itt Lissitzky vagy Tatlin nevét, és azt, hogy különösen Rodcsenkónak a “társadalom szolgálatába állított“ konstruktívizmusa nyújtott erre jó példát). A holland de Stijl csoport esetében aztán megint a puritán moralizmus, a kvázi vallásos program került elôtérbe (Mondrian a legjobb példa rá), noha a de Stijl-en belül is elôfordult, hogy egyik-másik mûvész “elbotlott“, és formatervezésre vagy architekturális feladatok megoldására adta a fejét.

E két egymásnak ellentmondó törekvés idônként egymásba fonódott, mert tagadhatatlan, hogy a technicista, tehát a formatervezéssel rokon ágazatok is egyfajta messianisztikus elkötelezettségre épültek, hiszen a gyakorlatot szolgáló mûvészetük még egyáltalán nem lehetett magátólértetôdô. A technikai kultúra magasabbrendûsége pedig olyan tanítás volt, amit prófétai buzgalommal követtek. Mindenesetre az 1910-es és 20-as évek konstruktívista törekvései együttesen elérték azt, hogy igen erôs tábort képezzenek, úgy hogy végül az ô eredményeikbôl kristályosodott ki a 20. század vizuális kultúrájának és forma-alkotó törekvéseinek az anyanyelve is.

Nehézségek csak a 20. század utolsó harmadában jelentkeztek, amikor mind a konstruktívista formák megváltóerejében való hit, mind pedig a szigorúan geometrikus és funkcionális design-iskola küldetéstudata alól kicsúszott a talaj – mégpedig azért, mert a század nem csak élt a konstruktívista törekvések eredményeivel, hanem egyúttal vissza is élt velük, illetve néhány évtized alatt felélte, kommersz áruvá hígította ôket. Az 1960-as évektôl kezdve sem a messianisztikus küldetés-tudatra, sem pedig a Bauhaus-féle józanabb programokra nem volt már többé szükség, hiszen amúgy is, nélkülük is minden “modern“ ruhába öltözött. Ebben a helyzetben legfeljebb a bôségben való lubickolás és a szemkápráztató játékosság megjelenítése számíthatott még sikerre, és valóban az történt, hogy a neo-konsruktívizmus iskolái, így a Vasarely féle Op-Art, vagy az illúzionista játékokat a mozgás különbözô szenzációival összekapcsoló Mobil-Art, és egész rokonságuk tényleg ezekre a hatásokra építettek. Akik pedig még mindig a konstruktívizmus morális erejében és erkölcsi magasabbrendûségében hittek, azok is csak úgy tudtak talpon maradni, ha közel maradtak ezekhez az újabb irányzatokhoz, és a mozgás, a szeriális motívumsorokban rögzített változás, illetve az idô múlásának és a formák változásának az egymással ölelkezô közös játékát, vagy a konstruktívizmusnak az akció-mûvészetben való feloldódását tették meg mûvészetük tárgyává. (Ezt a változást figyelhetjük meg a század utolsó évtizedeinek magyar mûvészetén belül is: Gáyor, Maurer, Mengyán, Halász, El Haszán, Csörgô, stb. egy olyan sort alkotnak, ami végül is “kivezetett“ a konstruktívizmusból.)

Ez a helyzet – durván fogalmazva – azt is jelenti, hogy a posztmodern korszak viszonyai között a konstruktívizmusra, mint küldetéstudattal ellátott mûvészetre, vagy mint igazi, az élet totális értelmezését magára vállaló avantgárd törekvésre nem volt többé szükség. És ekkor jelentkezett Saxon-Szász a maga archaikusan tömör, igen kevés színnel megalkotott, és ami a formák gazdagságát illeti, e téren is feltûnôen visszafogott alkotásaival!

Semmi illúzionizmus, de annál több kapcsolódás a tudományos világképhez, és egy “jobb“, “tökéletesebb“, illetve “komplexebb“ forma-rendszer kereséséhez – ez volt a devízája. Mindezek az erények a régi, a korai konstruktívizmus maximáira emlékeztetnek. Sôt, ami új bennük, nevezetesen, hogy a régi konstruktívizmus statikus világát dinamikusabb szemlélettel váltotta fel, az is a tudományos világképbôl érkezett, és ennyiben az is a klasszikus konstruktívizmus mentalitásához való visszatérést jelentheti. Ami mégis jelentôs különbség: az ô utópia-rendszere már nem a 20. század elejének a technikai kultúrájából táplálkozik, hanem a káosz és a harmónia határán egynesúlyt keresô jelenkori matematikai elméletekbe, például a fraktálok világába kapaszkodik bele. Ez természetesen egy új értékszemlélet gyümölcse, mégpedig egy olyané, ami komplex rendszerek új szemléletével rokon, és amire különben kevés példát lehet találni a jelenkor mûvészetében.

Mindez azt a benyomást keltheti, hogy Saxon-Szász arra törekszik, hogy a klasszikus konstruktívizmus normatív szemléletét a jelenkor sokkal bonyolultabb és áttételesebb utópáival helyettesítse. Mûvei ikon-jellegûek, de nem ikonszerûen mozdulatlanok vagy merevek, hanem mozgásra, változásra, egy-egy motívum továbbgondolására serkentenek. Ahelyett, hogy statikus ideogrammokat alkotna, olyan folyamatokat indít el a képeivel, amiknek a logikája tovább vezet a végtelenbe. Ez a végtelen azonban nem science-fiction filmekbe illô szenzáció, hanem transzcendens jellegû értékvilág. Azokkal szemben, akik a fraktálképekben az új szenzualizmus, vagy a (nem is annyira új) vizuális eklektika eseteit keresték, ôt a törvények jelenléte és maximalizmusra kötelezô ereje foglalkoztatja, s ezzel magyarázható a megalkuvást nem ismerô matematikai szigor is a képeken. Mindezzel Saxon-Szász a klasszikus avantgárd egyik fô jellegzetességét, a formák végletes letisztítását, a redukcionizmust elevenítette fel újra. De végeredményben mégsem a matematikai tömörség az, ami e szimbólikus nyelv mögött rejtôzik. A tudományos világképet csak hasonlaltként, metafóraként használja, hogy vele általánosítottabb dolgokról, emberi erényekrôl beszélhessen.

Amit Saxon-Szász értéknek tekint, az – valószínûleg – az önkorlátozásnak az a formája, ami elsôsorban az intellektuális élmények és a gondolati igényesség területén keres értékeket magának. Ha a felhasznált matematikai anyagtól kissé magasabbra emelkedünk, akkor azt találjuk, hogy a képek is ennek az igényesebb alapállásnak a jelképei. Velük Saxon-Szász olyan magatartást hangsúlyoz, ami egyaránt ellentmond a fogyasztói társadalom felelôtlen pazarlásának és az abból kifejlôdött informatikai társadalom illúzionizmusának és szenzualizmusának is. Ezeket a tartományokat útvesztôknek, labirintusoknak tekinti, és velük szemben olyan kozmosz kiépítésén fáradozik, aminek az értékrendszere sokkal puritánabb és aszkétikusabb természetû. Végeredményben ezt a missziót szolgálja képeinek a nehezen hozzáférhetô matematikai háttere is, mert arra tanít, hogy nem lehet olcsó eszközökkel eljutni az értékek közvetlen közelébe – aki intellektuálisan is birtokolni akarja ezt a mûvészetet és szeretne belépni e abba világba, amit ezek a képek csak jelképeznek, annak meg is kell szenvednie érte.

Mindezek a gondolatok és igények természetesen akár közhelyek is lehetnének, ha napjainkban általános elterjedtségnek örvendenének. De nem azok. Az a körülmény, hogy Saxon-Szász képeibôl mégis kiolvashatók, az ô kivételes adottságai mellett szól. Ellene csak egyetlen egy érvet hozhatnánk fel, azt, hogy meglehetôsen egyedül áll ezzel a teljesítményével – vagyis az “utópia“ szó használata itt nem csak költôi vagy filozófiai értelemben indokolt, hanem szociális és kommunikatív vonatkozásban is találó. Saxon-Szász János egy maga alkotta szigeten él, és ezt a maroknyi földrészt a tömegtársadalom média-világa veszi körül. Magánya egyrészt az egyetemes kultúra pillanatnyi helyzetével magyarázható, mert azzal függ össze, hogy az avantgárd lehanyatlásával az egyetemes képzômûvészet apályos, mi több, problematikus korszakába került, és lehet hogy csakhamar el is merül a tömeg-mûvészetek tengerében. De összefügg azzal is, hogy Saxon-Szász éppen Közép-Kelet Európában él, és ez az övezet még nem jutott el a “Kánaánig“, a fejlett ipari társadalmaknak ahhoz a fajta pazarló gazdagságáig, amely meghatározó erôvel van jelen sokak tudatvilágában. Itt még lehetséges az, hogy valaki a klasszikus avantgárd morális elkötelezettségét tekintse példaképnek, és ehhez a erkölcsi maximalizmushoz új tartalmakat keressen. Az az aszkétikus igény és maximalizmus, ami Saxon-Szász képeibôl sugárzik, ezért tûnik különlegesnek és kivételesnek.

Korai lenne mérleget vonni, és pozitív vagy negatív elôjelû végkifejlettre következtetni ebben a helyzetben. Mivel nem látunk a jövôbe, nem ismerjük az ott rejtôzô esélyeket sem. Saxon-Szász fiatal, sok ideje van még. Sok víz fog lefolyni a Dunán addig, amíg a korszakról, amiben ô is élt, kiderül majd, hogy milyen tendenciák gyôztek benne.