The Poly-dimensional Fields of Saxon-Szász
A creative artist between mathematics and the realm of “beautiful proportions”


When I first visited János Saxon-Szász, and his wife, Zsuzsa Dárdai, whom I had basically considered as representatives of electrographics before, it turned out at once that Jani Szász is not only a distinguished artist of the innovative, experimental electrographic trend, but also a par excellence painter. That is, his flat was filled with oil paintings, either ready or in the making. Most paintings were almost monochrome, merely combining two colours, the powerful tone of cadmium yellow and the flashy brightness of white. But it was not this that I found most stunning; rather the fact that, although the pictures were at first sight characterised by lucidly structured Constructivist compositions following the established style of geometric abstraction, they were not quite so! Behind the proportions that seemed so simple there lurked an unusual complexity, and this tension, so difficult to unravel, proved almost thrilling. And then, suddenly, it occurred to me what I was contemplating.—“Hey, these are fractals!” I exclaimed. And so they were too, which was a sensation not only because as an amateur scientist I had already been investigating this fairly new branch of mathematics for some ten years, but also because as an art historian I had never before found a successful application of fractal geometry in the creative arts anywhere in the world.
Namely, the visual presentation, and beauty of fractal geometry had not emerged from among creative artists. It was a gift of computer technology, and it astonished the world as colour technology became widespread in the 1980s. The mathematics behind fractals was also considered relatively novel, and initially it could only interest a narrow circle of experts. But then the figures appearing on the screen became unexpectedly colourful and rich. They conquered the most extreme fields of visual culture overnight, so to speak, and they grew so popular that for some time they even ousted Impressionist reproductions in exquisite bank and company calendars. Many people bought computers merely to be able to display on the screen or perhaps print out the overwhelmingly beautiful details of Mandelbrot's set. And those who were more familiar with mathematics, could discover new fractal algorithms and produce their “own” fractal geometric images.
But not even the virtuosi of digital technology and the craftsmen of visual culture went further than that—fractal images never became “art,” as the mathematical background for these interesting computer-generated figures proved all too complicated and these images, heavily depending on computer technology, remained the electronic “expressions” for certain mathematical calculations. Meanwhile, the amateur enthusiasm surrounding fractals has subsided, and fractal geometry (as well as chaos theory, the mathematical apparatus behind it) has retreated to its more specialised fields and its results have been incorporated into other branches of science. It is to Saxon-Szász's merit that as a creative artist he found a way to handle fractals; his achievement is hardly credible. Now that I wish to address his works more closely, I think it central that I should—at least in a sketchy way—explain the real nature of fractal geometry to the reader.
*
As a commonplace, we must start with the ancient Greeks. The origin of mathematics is rooted in the spiritual and economic life of ancient societies; thus, geometry was necessitated by territorial surveys (geometry itself means “land-measuring”), Pythagoras' theorem being an arch-example, describing as it does the proportions between the sides of a rectangle triangle. In all probability, ancient Greeks took this knowledge from the Egyptians, who had to measure land patches anew each year due to the floods of the Nile. In such circumstances, it must have been quite natural to observe that it is simplest to draw a right angle on the ground if one takes a rope and stretches it in a triangular shape so that the sides are 3, 4, and 5 length units, respectively. The perpendicular sides thus arising will surely have an angle of 90 degrees. Pythagoras' theorem is the generalisation to all rectangle triangles of this practical knowledge.
Another famous set of proportions that can be linked to ancient Greek philosophers is perhaps even more comprehensible. It is the teaching of “harmony”, the rules of harmonious tones. This set of proportions originated in the understanding that if a vibrating string is stopped down in the middle (that is, in a proportion of 2:1), a very exact regular interval, an octave emerges. All other consonant or harmonious intervals can be described according to proportions of whole numbers. The string may thus be divided at a proportion of 4:3, or 3:2, and the—according to Greek terminology, “symphonic”— intervals that arise will be fourths and fifths. In antiquity, entire cosmologies could be constructed on this basis, which tried to imagine the structure of the universe in agreement with the vibrating string, its harmonic proportions, and the ensuing “symphonic sounds”—their attempt is still reflected in the term “music of the spheres.”
An example of more complex systems of proportion is the golden section or, in Latin, aurea sectio. Here, a shorter line “a” has the same relation to a longer “b” as “b” has to the sum total of “a” and “b.” This can be described in the following formula: a/b=b/(a+b). Occurrences of the golden section as the most perfect and beautiful proportion can be found throughout the history of human culture; for it is strangely embedded even into our “rules of thumbs,” and geometric methods have been devised for its precise calculation ever since antique times.
An algebraic approach to proportions similar to the golden section did not emerge until much later. One such example is the 13th-century Italian mathematician Fibonacci (originally Leonardo Pisano). The Fibonacci series, which bears his name, is created if we set out from the beginning of the sequence of whole numbers, and we add up two consecutive elements to calculate the third one following after them (1, 1, 2, 3, 5, 8, 13, 21, 34, etc.). The beginning of this sequence is rather uninteresting, but if we check how later elements approximate the rules of the golden section, we will find that by elements 8 and 9 (21 and 34) the proportion is almost perfectly in keeping with this principle; 21:34 (that is, 0.6176) almost equals 34:(34+21) (0.6182). The Fibonacci sequence may have been the first mathematical object that drew one's attention to the fact that actions taking place in a progressive sequence are more than simple repetitions, and they may cherish creative forces.
Among the forms of nature one often finds examples that show such progressive repetition of the golden section or some other conspicuous set of forms and proportions in individual natural objects. The order of the branches of a tree; the network of a leaf's nervure, which becomes more and more minute near the edge of the leaf; or the laceration of the fern, repeated on a smaller scale at the edge of each fern leaf; as well as the widening or narrowing of the serpentinous line of a snail shell—all these constitute systems whose main feature is that although the size of the individual forms varies incessantly, the proportions and characteristic shapes of these forms remain so constant that their similarity overrides whatever differences there may be in size. At the same time we must acknowledge the importance of the possibility to group these forms and proportions in a regular sequence (just like Fibonacci's series), and the elements of the sequence will follow each other so regularly that they may effectively constitute an infinite sequence.
It seems that organic and inorganic nature creates things whose constituting forms recur in the selfsame object several times on a smaller or larger scale—that is, the shape of these elements is independent of a scale shift. Since such constancy (or “invariability”) of things could, in a wider respect, be conceived of as symmetry (objects having axial symmetry, for instance, are invariable with regard to the left- or right-side structuring of constituting forms), we could even put it thus: well, nature has its own geometry or symmetry, as most forms of nature are invariable to a shift of scale.
It may be conspicuous that even though human culture in past millennia had already known such sets of proportions—golden section being one of those—that essentially showed a repetitive nature at smaller and larger dimensions in “beautiful” objects (that is, a proportion that would in principle have been capable of leading to infinite sequences), yet this unique kind of symmetry was only appreciated statically by the humanity of former epochs, and its investigation never created a series of grades, or objects that could be dynamically developed and described in a mathematical way. Even in the fields of science or the arts, mankind has never created anything that would have addressed this actually very basic form of symmetry, scale-invariability, with the seriousness it really deserves. Mathematicians only succeeded in realising the real deep importance of scale-invariant sequences in the 20th century, more precisely in its last third, as computer technology developed dramatically. For this, one needed a far more dynamic world view than what one had had before—not to mention the computers capable of handling the technological complexities of extremely long (in theory, infinite) mathematical sequences. And when the representatives of individual branches of science started to look for forms being invariant to scale-shifts in their very fields of specialisation, almost the entire natural world turned out to be so. It is this strange type of symmetry that governs the organisation of the world, rather than the Euclidean geometry of old.
The shapes corresponding to this dynamic symmetry were, then, called “fractals” by Benoît Mandelbrot. The name derives from the Latin past participle “fractus,” meaning “broken.” It derives from the fact that a characteristic feature of forms built upon such sets of proportions is the peculiar nature of their outlines on a plane or their volume in space: they never have a fully two- or three-dimensional shape, rather a more irregular appearance, which tends to have blurred silhouettes, or “fractured,” “hollow” outlines—such as the hardly analysable shape of clouds, the multiple laceration of ferns requiring thorough observation, or the infinitesimal branching into microscopic regions of the lung of mammals. Since Mandelbrot's mathematical findings we can speak, for instance, of “one-and-a-half-dimensional” objects if a line thickens into hatching, or of, say, a “two-point-eight-dimensional” shape in the case of a spatial object turning into a foam form.
*
Let us compare these facts with the pictures by János Saxon-Szász.
The painting that helped me understand that he uses fractal geometrical forms, bore the title “Dimension Steps” (in that meaning of the word which is identical with the expressions “size change” or “gradual scale-shifting”). The starting point of this picture was a square, which Saxon divided into smaller parts by splitting one side into three; then he took the middle one from the possible smaller squares and went a step further, and repeated the same process with the next square that could be drawn along the inner edge of the missing middle square. Thence he could move on to another, even smaller square, and this process could have been continued ad infinitum. (There you have invariability to scale-shifting!)
It would, of course, be very difficult to come much further on these stairs, since the forms that emerge even after the very first steps make it hardly possible not only to carry out but also to think of their further sections. Saxon-Szász was thus content to apply this section three times to the original square (though each time at smaller dimensions) before he stopped. The logical steps of the creation of this painting can be illustrated in the following way:

The reader familiar with contemporary art could in fact say that this painting belongs to the geometric compositions following the “shaped canvas” style—after all, the missing square forms are literally cut out, that is, the edge of the picture is physically “shaped”). However, a visible characteristic of this picture provides us with an additional element: its dynamism almost serves as an imperative telling the observer to continue in his mind the creation of smaller squares emerging in the middle of the frame to infinity. One must admit that if one were to do so, this “chipped” edge would become ever more densely lacerated, and eventually one would even become unable to calculate accurately the length of this broken line—or else, one would be bound to declare that this length has grown infinite, since to the innermost point of the completed edge one could still attach an even newer, even smaller bay-like appendix, and in principle this process would never end.
Furthermore, the borderline thus arising fulfils in many respects the requirements of fractals, since it is nothing more than a representation of the notion that the original form recurs again and again within the same object, while its scale becomes ever smaller. The final motif is effectively nothing more than the repetition of one, basic form, independent of scale-shifting. As a curiosity, I must add that if Saxon were to apply this ever smaller division to all broken edges on the given side of his square, he would come to the variation of a classical case of fractal geometry, the so-called Koch curve. Here comes the first three steps of such divisions in Koch's curve and in “Saxon's curve”:

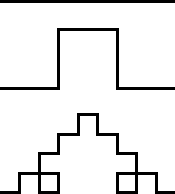
Koch curve	Saxon curve

Let me supplement this example with one more interesting fact. Mandelbrot, the best-known researcher of fractal geometry, gave as the characteristic parameter of fractals precisely that extent of fragmentation, which—as mentioned above—can be expressed in broken numbers. According to Mandelbrot's definition, the measure of “fractal dimension” can be calculated if we take the logarithm of a broken number whose numerator is the number of steps required for the particular degree of brokenness, whereas the denominator is the actual size of the object. In Koch's curve, the length of the final curve is only three units even after four steps (as one can see in the figure above), thus the fractal dimension of the curve is the logarithm of 4/3, which is 1.2619. If we apply the same procedure to “Saxon's curve,” we should observe that he achieved a form of a three-unit volume through five steps, so the fractal dimension will be the logarithm of 5/3, which is 1.4650. If we compare these two numbers, we will realise that the “oscillation,” the brokenness of the Koch curve—though overrides the simple world of one-dimensional lines, is nonetheless closer to the line than the almost one-and-a-half dimensional laceration of the “Saxon curve.” In other words, “Saxon's curve” comes closer to two-dimensional figures, that is, it “hatches” better.
Since fractals bearing broken numbers as fractal dimension would only become objects of physical reality if the actions leading to fragmented fractal forms—division or fragmentation—could indeed be continued ad infinitum. Ideally, any fractal form would take on infinite dimensions, through its fragmented, “porous” structure it would increase to such an extent both in microscopic and macroscopic realms that it would squeeze out everything else from the universe. This mental act is, of course, a typically human generalisation, and does not reflect the actual situation in nature, where fractal forms are bounded by the laws of the material world. In reality, all those several million fractals can exist side by side, or even penetrating each other, which, for example, any aerial photograph will reveal in connection with ever so small patches of the earth. (This interpenetrating fractal geometrical structure is, of course, invisible to the “naked eye.” Nevertheless, M. F. Barnsley, the famous American mathematician has devised a method with which satellite photographs showing an immense richness of detail can be condensed into a few thousand fractal formulae—for easier storage.)
The fact that even seemingly accidental aerial photos can be turned into fractals, that is, into absolutely regular and mathematically analysable shapes, proves that the overwhelmingly beautiful fractal forms published in books (as well as their relatives, Saxon-Szász's works) are highly “purified” and idealised forms, and as such are no different than other human concepts or cultural products brought forth by analytical thinking—the equally ideal and pure shapes of Euclidean geometry, for instance. The importance of this fact is not merely epistemological. As we are to prove later on, it is also significant from the point of view of aesthetics.
In order to understand the significance of Saxon-Szász's works, let us return once more to the history of fractal forms. As I have already mentioned, it is surprising that although nature is full of fractal-like forms, we would search in vain for such shapes in the past of human culture. Humanity, it seems, has learned to think along the very lucid and simple lines of Euclidean geometry. It appears that from all those few fractal motifs that have ever (accidentally?) been produced by man, the oldest one is the mosaic ornament in the 12th-century cathedral of Anagni, Italy. Namely, the decorative figures of that church are constructed from elements which in fact are perfect fractals, and whose counterparts were not produced before 1915, when the Polish mathematician Sierpinski created his own similar forms (Anagni mosaic / Sierpinski's triangle).

Mosaique. Anagni, chatedrale	Sierpienski triangle

For all his efforts, Mandelbrot, who was also keen on investigating the history of mathematics, for which purpose he consulted a huge library of art historical books and reproductions as well, could find but a handful of fractal-like images from the fields of culture. Looking at Leonardo's drawings about the Flood, or Hokusai's famous “Great Wave” woodcuts he thought he had found motifs similar to fractals, repeating elements on smaller or greater scales—but nowhere else. But mathematicians themselves had not come near fractal-like objects before the 19th century. Hausdorff from Germany and Poincaré from France researched mathematical sequences that have proved to show infinite fragmentation or complexity and thus fall into the category of non-linear mathematics. Their graphic representation results in fractals, too. Nevertheless, Poincaré called these clumsy inventions “monsters,” mathematical beasts,since they could not be treated with ease on the basis of either Euclidean geometry or other mathematical methods known at the time (i.e. differential or integral calculus). In his footsteps, however, and particularly in the years around 1900, there emerged a number of people who found similar “monsters” and created a series of mathematical and geometrical objects which can today be considered fractals (mention must be made, among others, of Georg Cantor, H. von Koch, Waclaw Sierpinski, or Giuseppe Peano and Gaston Julia).
In the end, however, it was only Mandelbrot who, in the 1970s, broke with the notion that these formations should be treated as obscure, monstrous things. For he had managed to develop a technique through which these infinitesimally fragmented (almost dust-like) forms could be described, their parameters measured. It was also him that first understood that the structuring logic of the natural world rests precisely on fractal geometry, a formal system that is invariable to scale-shifting. In the late-1970s and early 1980s he published his most important books on this topic; however, his writings discussing this new chapter of mathematics only became available in Hungary more than a decade later, and merely in a scattered way.
*
All the more interesting is the fact that János Saxon-Szász, who had been a high school pupil in Nyíregyháza in the 1970s, should, quite independently of these developments, have shown interest in the special forms of symmetry-changes, and the representation of scale-shifting in his very first written work. Among other things, his “Universe” (1979), a drawing he produced at the age of fifteen at the constructive summer symposium at Gönc led by Tibor Csiky and János Fajó, documents this interest.

János Saxon-Szász : Universe (1979)

He remained a regular visitor at the Gönc summer school (later removed to Encs) in the following years, and when he moved to Budapest in 1982, he carried on his work at Pesti Mûhely (“Atelier Pest”), creating graphic, plastic, and painted works, largely rooted in the spirituality of Constructivism. He applied for admission to the College of Applied Arts in Budapest, but as he was refused, he enrolled the Bánki Donát Technical College, with the explicit purpose of acquiring technical knowledge that he would be able to use in metal sculpture. And his composition “Structure” (oil on canvas, 1988) demonstrates that even in his Constructivist works from this period he investigated the scale-shifting of shapes.
In the nineties, he became a member of the international MADI movement led by Arden Quin (MADI is an acronym of Movement, Abstraction, Dimension, and Invention), whose free thinking and experimental attitude helped him understand, among other things, what possibilities may emerge if a painting leaves the form of the rectangular frame and takes on elements of other object-creation. It was through this that he eventually arrived at the notion of the “shaped canvas,” of “shaped” or formatted paintings.
As a mathematician, starting from Poincaré, Saxon-Szász might in the end have rediscovered what Mandelbrot had established just a few years before. In the event, however, due to the decisions he made after graduating from the technical college, and the different artistic circles and schools he was associated with, Saxon's artistic ambitions and innate mathematical gifts helped him elaborate his own system of forms (so like fractal geometry), which served as a basis for his creative activity and could be attached to geometric abstraction, an important tradition in art, rather than a more sterile understanding of mathematics.

János Saxon-Szász : Structure (1988)

Small wonder, then, that he elaborated his own terminology independent of the international context of mathematical research, more related to, say, the language of Constructivism. Among the differences the most important and most characteristic one is the fact that Saxon-Szász consistently uses the word “dimension” in the sense of “scale,” or “order of magnitude,” and not in the way one uses it in connection with two-dimensional planes or three-dimensional space. Thus when he mentions poly-dimensional fields, these must be conceived of as working spaces where forms are repeated in smaller and larger dimensions, and hence each and every motif is subordinated to the gradated rhythm of scale-shifting (change of dimension), which pervades the entire work. (No one should think of the preposterous idea of encountering science-fiction-like four- or five-dimensional objects.)
Scale-shifts themselves, as well as the repetitious logic enabling them, are known as “iterations” in mathematics (hence the expression “iterative mathematics/geometry”). Since the early 1990s, Saxon-Szász has created a series of pictures which are no longer experiments or speculative questionings; any mathematician would see their connection to iterative geometry or fractals at once. On the other hand it is equally sure that the selfsame works by Saxon-Szász will nonetheless be considered products of the creative arts by any art critic—the only thing added would be that fractal geometry has turned into ideograms in these pictures, i.e. it takes on a symbolic role as it returns. Saxon-Szász has succeeded in bringing together in perfect harmony two realms that lie far from each other, namely mathematics and the communicative forms of creative art.
In the nineties, his works started to arouse world-wide interest; he was invited to exhibit and he also received scholarships. One of his most important experiences proved to be the invitation of the Espace de l'Art Concrete in Mouans-Sartoux, France. He not only had the opportunity to work in an atelier for five months, but he was also commissioned to lead a creative circle where he had to put his notions into words, and practice. As a result of this scholarship and the work of these months the multilingual publication “Dimension Crayon” appeared, supported by the Espace de l'Art Concrete and MADI. In this booklet Saxon-Szász expounded his programme under the title of “Poly-Universe”—this text can be considered both an artistic manifesto and a proclamation discussing a peculiar variant of fractal geometry.

János Saxon-Szász : front page of the publication Dimension crayon

The fact that Saxon-Szász immediately writes about a kind of universe, throws light on two elements which are utterly central in his entire oeuvre. One of these may be derived from fractal geometry itself, since it follows from the logic of infinite sequences and their features. For if iterative geometry, in theory, works with sequences calculable ad infinitum, then—as already mentioned—each model will, at least in principle, have infinite extension. And this maximal principle may indeed give one the impression that a single fractal is, at least in one's mind, a separate world, a complete universe in which exclusive laws are at work.
The other characteristic is a consequence of these highly idealised circumstances: if a model (a work of creative art, as it is in our case) can be taken for the iconic representation of a possible world within its own logical system and is like a thought-out universe, then the models (or pieces of art) thus arising will become utopias, in the sense used by Thomas More himself: islands with a symbolic meaning, standing opposed to the real world as its possible alternatives, “better” variations.
There is a work in Saxon-Szász's oeuvre, which could be called his most complex piece so far: his “Poly-Dimensional Chess,” which perfectly illustrates this utopian island function. This three-dimensional object models a chess board, whose fields become proportionately smaller as one proceeds further and further away from the centre of the board. The decrease of their size follows a constant scale-shift. This, of course, also means that each move in this universe is synonymous with a change of the figures' size as well. In fact, if we accept this board as a model of universal appeal, then the rhythm of scale-shifting will also prevail over a great deal of other things in addition to the figures; it will constrain all those objects or persons who come into contact with the board—eventually even the players who sit down for a game. So the entire world can be summoned to this chess board, while this separate universe extends into infinity according to its own laws, and at the same time, for onlookers, it becomes infinitesimally small only a few inches from the edge of the board:

JánosSaxon-Szász : Dimension chess

What is the moral of all this? Saxon-Szász has chosen the word universe in order to imply that his pictures should really be taken for possible worlds, models of universal validity, which brings him into the distinguished company of avant-garde utopias. Let me merely refer to the origins of Malevich's oeuvre, the Black Square, which Malevich intended as a model for a possible new cosmos; and let me mention his Suprematist manifestoes, in which the system of similar forms occurs as a de facto world model. I should also point out that, accordingly, Malevich not only created graphic works and paintings, but also spatial forms, Suprematist architecture—as though he had really wanted recreate the world. Mondrian had similarly universal claims when he appeared with his specially structured paintings within the Constructive tradition. And Le Corbusier went as far as to hope to plan entire cities (or even more countries, or a whole new globe) within his own utopian vision, whose model—and this is very interesting!—he also furnished with a basic set of proportions; his “modulor” was founded on a combination of the golden section as well as human proportions.
It is the icing on the cake that researchers investigating the more complex forms of fractal geometry—fractals operating with so-called period doubling—discovered a constant “modulor,” which can also serve as a model. This constant, Feigenbaum's number (Mitchell Feigenbaum, d=4.669201…), whose importance can only be compared to that of p, was dubbed the “universal constant” by mathematicians, as it provides the key number to more complex objects, events, structures and proportions in a way that is valid for the entire universe; this key number defines which place the threshold of proportion where the change or leap critical for the scale-shift occurs has in the sequence of numbers. (It can be proved mathematically that scale-shifting is only possible in proportion with “d” in Mandelbrot's set as well as in any other complex sequence or fractal making use of involution and recursive arithmetical techniques. This also means that the validity of “d” is as exclusive as that of p with regard to a circle and its radius.) Although Feigenbaum's number only applies to the physical world, we could say that sometimes it leads to such fantastic human reactions and conclusions that these speculations no longer seem scientific theories, rather the elements of general human culture. And this blurring of borderlines works vice versa as well: the works of Saxon-Szász belong to the world of creative art, and yet they are created in a way that in their composition such proportions, or “modulors” play the central role which are based on a strict scientific system. The fact that in spite of all this Saxon-Szász has remained a creative artist, is due to the overwhelming cultural function of his works. Even in his partial solutions one can easily discover many elements that can only be explained in relation to the traditions of painting.
One of the most intriguing formal elements which explain why his poly-dimensional compositions never turn into mere illustrations in spite of their similarity to fractals is the “co-planal” technique (“auxiliary planes”) he uses. For when Saxon-Szász has iterated a geometric form and grouped the emerging shapes, he may still not consider his work complete; he takes the opportunity to provide a “background” to his composition by linking the corner points and bridging the gaps (see the gray fields):

This procedure is an arbitrary move from the point of view of mathematics, but aesthetically speaking it is something extraordinary from the vantage point of the cultural background of these paintings, since this is how the work is turned into an icon, an image of symbolic meaning, and this is how it receives its rich symbolic aura that enables it to take on an additional sacred function. In Saxon-Szász's works this quasi-sacred element is a utopian meaning—it emphasises his aim that his works should define norms and laws and serve as symbolic models for possible worlds. Once again I must call upon Malevich and the iconic structure of Suprematist pictures as an analogy.

János Saxon-Szász : Polidimenzional black square

It very seldom happens that a geometric form capable of iteration should be suitable as an icon on its own. If we find any, it is because it is formally related to the genre of the icon. One example can be the square, as it has the shape of the wooden board. On one occasion, Saxon-Szász did indeed take Malevich's Black Square as his starting point, and gave his work the title “Poly-dimensional Black Square.” The sides of this square are divided in a 1:5 proportion, and this is the scale-shift that leads to the creation of the “fringes” surrounding the central shape. Saxon applied this division to the picture three times. The outline of the consequent lacerated form is related to the inner borderlines which could be retrieved from the “Dimension Steps” mentioned earlier on (Poly-dimensional Black Square).
(An aside: the fractal dimension of the outlines can be calculated here as well. Here we have eleven steps for a change of 5 length units; the result is hence log [11/5], that is, 1.4899.)
Browsing among Saxon's works, one finds a whole series of compositions which are the result of the iteration of not one but at least two geometric forms. These most often feature angular shapes and curves that are embedded in one another, for the contrast of such forms is the sharpest, and this gives additional visual richness to the images. Saxon-Szász calls such compositional schemes, created from several basic elements “mixed forms,” as opposed to the “pure forms” composed from just one starting shape (Mixed Forms).
Such complex iterations are known in mathematics as well. Nevertheless, Saxon-Szász does not follow these mathematical types; he only moves closer to nature when he uses “mixed forms,” because—as I have already mentioned—true as it is that the formal treasury of our environment can be analysed into a great number of fractals, still it is very rare that one should find among these “pure forms” or “unifractals” that could directly be transferred into fractal colour picture books. There are many random (that is, accidentally encoded) elements in the codes of the shapes to be found in the real world. Moreover, there are many natural forms which, if we try to disentangle them, defy our attempts, and show that the logic of their structure can only be unravelled by means of multiple decoding, the use of several combined sets of proportions.
To all that has so far been said we may add as a supplement that from time to time Saxon-Szász also creates works whose mathematical background cannot be interpreted according to fractal geometry, but these works also emerge from his playing with different proportions. Such are certain form sequences that retain the volume of the original shape, but gradually change the proportion of width and length. In such a case a composition may stretch, as though it complied with the sucking force of a “black hole” known from cosmology and were endangered by transmutation into “singularity,” where every object extends into a thread thinner than a rail, but extremely long. Although such compositions, their shape being rather lengthy, hardly fit the pages of a booklet like the present one, we have tried to bring in an example among the reproductions, all the more so, because it is likely that the artist will continue to follow his instincts and investigate the extremes of playfulness that this kind of game with proportions may allow him.
So much, then, about the direct relationship between fractal geometry and Saxon-Szász's art. These examples, however, have not taken us beyond the technicalities of his art and never ventured into realms other than the mathematical background for his works. But the artistic output of Saxon-Szász is a permanent cultural achievement within the creative arts, and although what has been said so far is necessary for us to find the right place for his art in a wider context, that context cannot be complete without addressing questions of the more expanded world of the creative arts.
*
Much mention has already been made of the importance of Constructivist traditions, since the activity of Saxon-Szász is, after all, related to this chapter of 20th-century art history. It is another question, however, how far this almost hundred-year-old tradition can still be considered alive, and if it has any currency, in what form or validity it can incorporate Saxon's highly individual achievements.
The century-long history of Constructivism can be divided into several chapters, but effectively it is only two, rather sharply opposing tendencies that have struggled within it, taking turns in having the upper hand.
The first such tendency was explicitly moral in its content, and ideological in its nature; that is, it emphasised a normative, almost religiously messianistic programme. It denied the importance of the visible forms within the world, and it focused on give expression to the spiritual world lying behind natural forms. In keeping with this, it placed into the centre of art emblems reduced to simple forms, and iconic symbols, making them serve moral and spiritual values. In the very beginning, in the art of Malevich, this ideological content had already become dominant, so much so that the geometrically organised, “technicistic” formal language of Suprematist works could have appeared of secondary importance. (These geometric forms did not really originate in the world of technology, but in the ornamental elements of Russian folk art, as well as the reduced, geometric formal language of orthodox icon painting.)
The other current stressed the importance of tasks within everyday practical life and tried to make a reduced, geometric art serve these very tasks as well. This concept found its clearest expression in the programme of the Bauhaus (among others: Gropius, Moholy-Nagy, Marcell Bauer, etc.). But even within the group of Russian Constructivists there was a fraction that took design and the solution of practical tasks of everyday life as its main mission (let us mention Lissitzky or Tatlin, and the example of Rodchenko's Constructivism, which “served society”). Then, in turn, the Dutch De Stijl movement returned once more to a puritan morality, to a quasi-religious programme (Mondrian being the arch-example), although even within this group it sometimes happened that one or another artist “tumbled,” and undertook missions of design or architectural tasks.
At certain times, these two opposing tendencies became intertwined, for it is undeniable that even technical, that is, design-related branches were based upon a type of messianistic devotion—obviously, their art serving practical purposes could not be self-evident as yet. In fact, the superiority of technical culture was a teaching which they followed with prophetic enthusiasm. In any case, together the Constructivist strivings of the 1910s and 20s achieved the creation of a very firm camp, and in the end it was their efforts from which the mother tongue of 20th-century visual culture and form-giving crystallised.
Difficulties only arose in the third part of the 20th century, as both the faith in the redeeming power of Constructivist forms, and the missionary zeal of the strictly geometric and functional design-school were misplaced—for no other reason than the fact that the century not only used the achievements of Constructivist tendencies, but also abused them, and in a few decades it devoured them, turning them into commercial goods. From the 1960s onwards, neither the messianistic enthusiasm, nor the more sober programmes of the Bauhaus were needed, since even without them, everything was dressed in “modern” clothes. In such a setting, only the presentation of overflowing abundance and flamboyant playfulness could lead to some success, and indeed it happened so that the schools of Neo-Constructivism (thus Vasarely's Op-Art, or Mobile Art, connecting illusionist games with various sensations of movement) and all their “relatives” set off from these effects. And even those who still believed in the ethical superiority and moral power of Constructivism could only stay alive if they kept pace with these new tendencies, and they concentrated their art around movement, and change recorded in serial motif sequences; or the passing of time, and the changing of forms in a playful hubbub; or again Constructivism dissolved in a kind of action art. (This development can be traced in the Hungarian art of the last decades of the 20th century as well: Gáyor, Maurer, Mengyán, Halász, El Haszán, Csörgõ, etc., formed a series of artists, which eventually “led the way out” from Constructivism.)
This situation—if we put it roughly—also means that among the circumstances of the Post-Modern era one no longer needed Constructivism, an art form with a mission, or an avant-garde tendency in the real sense of the word, undertaking to give a total explanation for life. And at this point Saxon-Szász came forth with his works of archaic terseness, subdued and scarce colours, and, as regards formal elements, equally modest proportions!
No illusionism, but plenty of connections to a scientific world view; a search for “better,” “more perfect,” and “more complex” formal systems—these were Saxon's currency. These virtues resemble the maxims of old, early Constructivism. In fact, even what innovation it offers as opposed to the old, static Constructivism, namely, a more dynamic approach, derives directly from its scientific attitude, and as such it also points back to the mentality of classic Constructivism. An important difference, however: Saxon's utopian system no longer stems from the technical culture of the early 20th century; contemporary mathematical theories, notably the world of fractals, form its foundations. These theories, like his artistic approach, are searching for an equilibrium on the border of chaos and harmony. This, of course, is the fruit of a new appreciation of values, which is related to the new view of complex systems, and which has few counterparts in the art of the present.
All this may lead one to believe that Saxon-Szász attempts to replace the normative approach of classic Constructivism with more complex and indirect utopias of the present day. His works are iconic, but not iconically static or rigid; they stimulate one to move, to change, to think over one or another motif. Instead of creating static ideograms, he creates images that start processes whose logic leads one on towards infinity. This infinity, however, is not a sensation of science-fiction films, but a world of transcendental values. As opposed to those who looked for new sensualism or (not even so new) visual eclecticism in fractal imagery, he is interested in the presence and maximalising power of laws, and this is where the uncompromising mathematical strictness of his pictures derives from. Through this, Saxon-Szász has revived a main characteristic of the classic avant-garde, that is, the infinite purification of forms, or reductionism. In the end, however, it is not mathematical terseness that lies behind this symbolic language. He only uses his scientific world view as an analogy, a metaphor, in order to communicate more general things, human values through them.
What Saxon-Szász considers a value is—in all probability—that form of self-limitation, which searches for its own values first and foremost in the fields of intellectual experience and high mental demands. If we slightly raise our horizons from the mathematical material used here, we will find that the images themselves are also emblems for this more demanding basic attitude. Through them, Saxon-Szász emphasises an approach, which contradicts both the irresponsible wastes of consumer society and the illusionism and sensualism of the ensuing information society. He considers these realms as labyrinths or dead ends, and he works on a cosmos whose set of values is far more puritan and ascetic. All in all, it is this very mission the hardly accessible mathematical background of his pictures also reinforces, since it teaches one the lesson that it is impossible to come near real values through cheap devices—who wants to possess his art intellectually and to enter the world these pictures merely symbolise must first undergo suffering.
These thoughts and demands could, of course, be little more than commonplaces, if they were generally established in our time. But they are not so. The fact that they can still be deciphered from Saxon-Szász's pictures proves his extraordinary gifts. Only one argument could be brought up against him, namely the fact that he stands on his own with his achievement—in this way the use of the word “utopia” is not only justified from a poetic or philosophical point of view, but also in a social and communicative respect. János Saxon-Szász is living on an island he has created himself, and this tiny patch of land is surrounded by the media world of mass society. Saxon's solitude can on the one hand explained by the momentary situation of universal culture, since it is connected to the fact that after the decline of the avant-garde, universal art has entered an ebbing, what is more, problematic epoch, and it may soon sink altogether in the ocean of mass arts. But on the other hand it is also related to the fact that Saxon-Szász is living in Eastern Central Europe, and this region has not yet made it to the “Land of Promise,” to the wasteful richness of developed industrial societies, which is a powerful factor in the minds of many. Here it is still possible that someone should take as a role model the moral devotion of the classic avant-garde and find new meaning for this ethical perfectionism. This is the reason why the ascetic demand and perfectionism beaming forth from the paintings of Saxon-Szász seems so special and exceptional.

It would be premature to draw the balance and refer to positive or negative outcomes at this very moment. Since we do not see into the future, we do not know the chances lying there either. Saxon-Szász is young, he has plenty of time. It will be a long time before the epoch that he himself has been a part of can be evaluated, and one can tell which tendencies came out victorious from it.


Bibliography

Barnsley, Michael F. (1993). Fractals Everywhere. Second, enlarged edition. Academic Press.

Behr, Reinhardt (1989). Ein Weg zur fraktalen Geometrie. Ernst Klett Schulbuchverlag.

Cramer, Friedrich (1989). Chaos und Ordnung: Die komplexe Struktur des Lebendigen. Stuttgart: Deutsche Verlags-Anstalt.

Fokász, Nikosz (1999). Káosz és fraktálok: Bevezetés a kaotikus dinamikus rendszerek matematikájába – szociológusoknak. [Chaos and Fractals: Introduction to the Mathematics of Chaotic Dynamic Systems—for Sociologists.] Budapest: Új Mandátum Könyvkiadó.

Fokász, Nikosz (ed.) (1997). Rend és káosz: Fraktálok és káoszelmélet a társadalomkutatásban. [Order and Chaos: Fractals and Chaos Theory in Social Research.] Budapest: Replika Kör.

Gleick, James (2000). Káosz: Egy új tudomány születése. [Chaos: The Birth of a New Science.] Budapest, Göncöl Kiadó.

Hermann, Dietmar (1994). Algorithmen für Chaos und Fraktale. Bonn–Paris–Reading, Mass.: Addison-Wesley.

Mandelbrot, Benoit (1982). The Fractal Geometry of Nature. New York: W. H. Freeman and Co.

Peitgen, Heinz-Otto & Dietmar Saupe (1988). The Science of Fractal Images. New York–Berlin–Heidelberg: Springer-Verlag.

Peitgen, Heinz-Otto & Peter H. Richter (1986). The Beauty of Fractals: Images of Complex Dynamic Systems. Berlin–Heidelberg–New York–Tokyo: Springer-Verlag.

Perneczky, Géza (1998). Fraktálok és eseményminták. [Fractals and Event Patterns.] Budapest: Kijárat Kiadó, Teve sorozat.

Prusenkiewicz, Przemyslaw & Aristid Lindenmayer (1990). The Algorithmic Beauty of Plants. New York, etc.: Springer-Verlag. (These are the fractal representations which Saxon-Szász's works approximate most closely.)


List of pictures / Képjegyzék
(page):
22        Universe / Univerzum 1979–80, ink and serigraphy, 50x50 cm
29        Dimension Chess / Dimenziósakk 1998, oil on wood, 152x152x120 cm
49        Structure / Struktúra 1984–88, oil on canvas, 100x160 cm
50        Oscillo-circle / Rezgõkör 1989, oil on canvas, 90x100 cm
51        Ideon Threads / Ideonfonalak 1991, oil on canvas, 90x110 cm
52        Fight / Harc 1993, oil on wood, 100x100 cm
53        Micro-Macro Energy Levels / Mikro-Makro energiaszintek 1993, oil on wood,
        100x130 cm
54        Condensation / Sûrítés 1992, acryl on wood, 55x100 cm
55        Dimension Gates / Dimenziókapuk 1994, oil on wood, 60x140 cm
56        Space / Ûr 1992, acryl on wood, 43x100 cm
57        Dimension Keys / Dimenzióbillentyûk 1994, oil on wood, 62x96 cm
58–59        Meditative Structures I, II / Meditatív struktúrák I., II. 1995, oil on wood, 120x120 cm
60        Planar Eclipse / Síkfogyatkozás 1988–96, oil on wood, 100x100 cm
61        Dimension Steps / Dimenziólépcsõk 1996, oil on wood, 100x100 cm
62        Cosmic Oscillations / Kozmikus rezgések 1996, oil on wood, 71x200 cm
63        Dimension Condensation I, II / Dimenziósûrítés I., II. 1996, oil on wood, 28x200 cm,
        41x200 cm
64        Yes-No / Igen-Nem 1997, oil on wood, 60x100 cm
65        Immaterial Transit / Immateriális átjárás 1997, oil on wood, 152x152 cm
66–67        Poly-dimensional Field / Polidimenzionális Mezõ 1998, oil on wood, 350x190x5 cm
68–69        Dimension Aerials I, II / Dimenzióantennák I. II. 1999, oil on wood, 26x200 cm,