A hiperbolikus síkgeometria szemléltetésére és relatív ellentmodás-mentességének az igazolására készültek a hiperbolikus sík euklideszi modelljei, melyek közül a két legismertebb a Cayley - Klein - féle ill. a Poincaré - féle körmodell. Ezek a modellek arra is alkalmasak, hogy segítségükkel az abszolút geometria fogalmait, tételeit kissé más megvilágításba helyezzük azzal, hogy a szokásostól eltérő módon fogjuk őket szemléltetni.
Egy ilyen modell megismerése előtt érdemes elgondolkodnunk azon, hogy mit is jelent valójában a szemléltetés, vagy modellezés. Tekintsünk pl. egy magyarázkodást nem igénylő matematikai fogalmat, a kör fogalmát. Amikor a papírra, képernyőre, vagy akár a homokba rajzolunk valamit, amire azt mondjuk, hogy ez egy kör, akkor lényegében modelleztük a tudatunkban absztrakciók sorozatával kiépített fogalmat. Az sem számít, ha ez a kör inkább egy krumplira hasonlít, lényeg az, hogy miközben a rajzot nézzük, a modellezett fogalomra, a körre gondoljunk. A modellel szemben támasztott egyetlen követelmény, hogy a vizsgált jelenség szempontjából ugyanazokat a tulajdonságokat tükrözze, mint amelyeket maga a vizsgálat tárgya, vagy jelen esetben a vizsgált fogalom.
Ha a megszokottól eltérő modellel szemléltetünk egy fogalmat, amely azonban ugyancsak jól tükrözi a vizsgált – absztrakt – tulajdonságokat, akkor joggal számíthatunk arra, hogy ezzel jobban sikerül megismernünk a vizsgált fogalom lényegéből (és nem a rajzolt modellből) adódó tulajdonságokat. Például, ha azt a kijelentést – tételt – akarjuk szemléltetni, miszerint
| ha
egy háromszögnek van két egyenlő oldala, akkor van két egyenlő szöge is,
|
Már ezért is érdemes egy a szokásostól eltérő modellezési lehetőséggel megismerkednünk. Így ugyanis világosabbá válhat a kapcsolat az axiomatikus felépítéssel kiépített és a szemléletünk alapján elfogadott, ill. elfogadható geometriai összefüggések között.
A nem euklideszi geometriák szemléletessé tétele összetettebb feladat. Ha pl. a síkot – mint fogalmat – egy körlappal modellezzük, magát a kört pedig egy a papírra, vagy jelen esetben a képernyőre rajzolt ábrával, akkor ebből az ábrából egy kettős absztrakció révén jutunk el magáig a vizsgált fogalomig. Reméljük, hogy ez a kettősség nem fogja zavarni a program felhasználóit.
A hiperbolikus geometria euklideszi modelljei közül most a Poincaré - féle körmodellel – a továbbiakban P-modell – foglalkozunk, amelyben a szög metrikája a közismert euklídeszi – és egyúttal hiperbolikus geometriai – metrika. A P-modellnek ez az ún. szögtartó tulajdonsága az, amely talán személetesebbé teszi a többi modellnél.
A modell bevezetéséhez meg kell először ismerkednünk egy a középiskolában nem tárgyalt, de a középiskolai ismeretekkel könnyen kezelhető geometriai transzformációval, az inverzióval.
A P-modellen a (hiperbolikus) síknak egy (az euklideszi síkba rajzolt) nyitott körlap felel meg, amelyhez eszerint a körvonal pontjai nem tartoznak hozzá. Nevezzük a modellt meghatározó kört a P-modell k(O,r) alapkörének. A hiperbolikus sík egyeneseinek a megfelelői A P-modell alapkörét merőlegesen metsző köröknek az alapkör belsejébe eső ívei, ill. a k kör O -ra illeszkedő átmérői lesznek.
Amennyiben a program menüpontjainak
megfelelő sorrendben szeretnénk haladni, elsőként vizsgáljuk
meg, hogy miként lehet a legegyszerűbb geometriai
alakzatokat megjeleníteni ezen a modellen. (Ismételten
felhívjuk olvasóink figyelmét arra, hogy célszerű párhuzamosan futtatni
a programot, és olvasni ezt a leírást.)
Miután programunk segítségével tettünk egy jó nagy körutat a hiperbolikus
geometria világában, vegyük szemügyre újból a modellünket, vizsgáljuk meg,
hogy milyen - a látvány szempontjából meghatározó - változtatásokat
végezhetünk a modellen, hajtsunk végre ilyen változtatásokat, és
ezekkel az adatokkal ismételten járjuk be a már látott menüpontokat.
A tanulságok magukért beszélnek.
Lássuk tehát programunk utolsó - de talán legfontosabb - menüpontját..
Gondoljunk arra, hogy ha valaki azt mondja, vegyünk fel egy a síkban egy kört, akkor még nincs értelme arról beszélnünk, hogy ez a kör kicsi, vagy éppenséggel túl nagy. Ugyanis nincs " mihez képest" kicsinek, vagy nagynak vélnünk.
A képernyő méreteihez viszonyítva nagy kör mindössze azt jelenti, hogy olyan részleteket is megfigyelhetünk a kapott rajzon, amelyre egyébként technikailag nem nyílna lehetőségünk. Pl. az alapkört (a képernyőhöz viszonyítva) növelve fel tudunk venni az alapkörhöz viszonyítva kicsi háromszögeket. Így meg tudjuk figyelni, hogy ha az egybevágósági transzformációkat – melyek nem igénylik a szög- , vagy távolságmetrika megadását – a modell origójának a közelében, elég kicsi háromszögekre alkalmazzuk, rajzaink egyre inkább megközelítik az euklídeszi geometriában megszokott rajzokat. Figyeljük meg, hogy egy ilyen " kicsi" háromszögnek a defektusa egyre jobban közeledik a nullához.
Az alapkör sugarát növelve technikailag lehetőségünk nyílik arra is, hogy a távolság-metrika alapjául (tetszőlegesen) választott egység az alapkör sugarához viszonyítva egyre kisebb legyen. Így megfigyelhetjük, hogy a koordináta-rendszerünkben ábrázolt függvények rajza egyre jobban közelít a megszokotthoz.
Képzeljük el, hogy most a P-modell alapkörének – az egységnyinek választott szakaszhoz képest – nagyon nagy a sugara, mi pedig itt az origó közelében ábrázolunk függvényeket, szemlélgetjük az egybevágósági transzformációkat. Épp úgy nem érzékelnénk az euklídeszi és a hiperbolikus geometria közötti különbséget, mint ahogy egy szobában ülve azt sem érzékeljük kézzelfogható módon, hogy a föld gömb alakú.
Természetesen, ha ezt a " nagy" kört a képernyőhöz képest eltoljuk, és a körvonal közelében vizsgálódunk, rajzaink továbbra is szokatlanul viselkednek. Maga a P-modell pedig egyre jobban megközelítené a hiperbolikus sík egy másik, ugyancsak Poincaré által készített modelljét, az ún. félsík modellt, melyben a hiperbolikus síknak az euklídeszi sík egy félsíkja felel meg, az egyeneseknek pedig olyan félkörök, melyek középpontja a félsík határegyenesére illeszkedik.
Az euklídeszi és a hiperbolikus geometria sajátosságait összevetve
hadd hívjuk fel még egy érdekességre a figyelmet. Íme három mondat, melyek
egyike az abszolút, másik csak az euklídeszi, harmadik csak a hiperbolikus
geometriában érvényes:
| A szögmérés abszolút. |
| A távolságmérés relatív |
| A távolságmérés abszolút. |
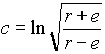 értékkel jellemezhető, ahol e
a tetszőlegesen felvett egység, r a modell alapkörének sugara.
értékkel jellemezhető, ahol e
a tetszőlegesen felvett egység, r a modell alapkörének sugara.
Futtassa a programot a Windows alatt. Ha egyszínű nyomtatója van, állítsa a rajz színét fekete-fehérre. Miután a megfelelő rajzot előállította, nyomja meg a Print Screen billentyűt. Ezzel a Windows vágólapjára helyezte a rajzot, amely azután bármelyik Windows alatt futó rajzolóprogrammal, pl. a Paint -tel tovább szerkeszthető.