Függvényábrázolás a hiperbolikus síkon

Mint láttuk, abszolút geometriai eszközökkel, így a hiperbolikus síkon is könnyen fel tudunk venni egy számegyenest, amelynek a modellezése P-modellen szintén problémamentes. Felvethető az a kérdés is, hogy miként lehetne az euklídeszi geometria Descartes - féle koordinátarendszeréhez hasonló rendszert készíteni a hiperbolikus geometriában.
 
A Descartes-féle koordinátarendszer feladata az volt, hogy minden valós számpárhoz kölcsönösen egyértelműen hozzárendelje az euklídeszi sík egy pontját. Amikor egy függvényt lerajzoltunk, tulajdonképpen a függvény által egymáshoz rendelt számpároknak megfelelő pontok halmazát rajzoltuk le. 
 
Most a feladatunk összetettebb: A tetszőleges (x,y) számpárhoz először alkalmas módon hozzá kell rendelnünk a hiperbolikus sík egy pontját, majd meg kell adnunk az ennek megfelelő pontot (illetve ennek az O origójú Descartes-féle koordinátarendszerben vett  koordinátáit) a P-modellen. Végül, amennyiben mindezt számítógépen kívánjuk szemléltetni, ezt át kell írnunk a képernyő koordinátarendszerébe, az ábrázoláshoz szükséges formába. Ez utóbbi azonban már nem matematikai, hanem számítástechnikai probléma.
 
A Descartes - féle koordinátarendszer lényegében két, egymásra merőleges számegyenesből áll, melyeken (többnyire) ugyanakkorák az egységszakaszok. Az (x,y) számpárok és az euklídeszi sík pontjai közötti hozzárendelést két különböző módon is elérhetjük.

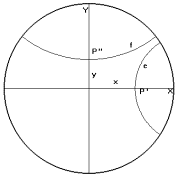
Az egyik út: Kijelöljük az egymásra merőleges X és Y számegyeneseken az x és y számoknak megfelelő P' és P" pontokat, majd az ezekre illeszkedő és az X ill. Y egyenesekre merőleges e és f egyenesek metszéspontjaként kapjuk P  -t. 

 
 

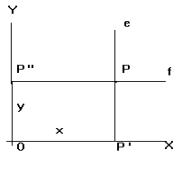
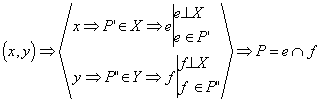
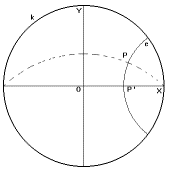
A másik út: Kijelöljük az X  tengelyen az x abszcisszának megfelelő pontot, majd az erre illeszkedő és az X -re merőleges egyenesen (az azonos abszcisszájú pontok mértani helyén) kiválasztjuk azt a P pontot, melyre a P'P szakasz előjeles hossza y . 

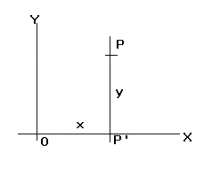
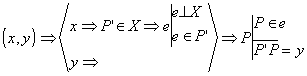
Az euklídeszi geometriában az OP'PP" téglalap rendelkezik azokkal a tulajdonságokkal, amelyek e két út egyenértékűségét biztosítják.

Mindez nem így van a hiperbolikus geometriában. Ha ott ugyanis az első utat választanánk, előfordulhatna elég nagy számok esetén , hogy a tengelyekre merőleges egyenesek nem metszenék egymást. A második utat választva viszont az azonos ordinátájú, tehát az X tengelytől azonos távolságra lévő pontok mértani helye egy hiperciklus lesz. Így jutunk az egész abszcisszájú, ill. egész ordinátájú pontok kijelölésével ahhoz a rácshoz, amellyel már találkozhattunk az eltérő sugársorok bemutatásánál. 

 
 

A koordinátarendszert meghatározó két egymásra merőleges egyenesnek választhatnánk a P-modell két tetszőleges, egymásra és az alapkörre merőleges körívét, azonban ahhoz, hogy rendszerünk lehetőleg hasonlítson az euklídeszi geometriában megszokott koordináta-rendszerre, válasszuk koordináta-tengelyeknek az alapkör két, egymásra merőleges átmérőjét.

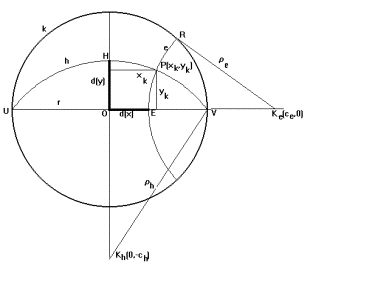
Mind az azonos abszcisszájú pontok mértani helye (egyenes) mind az azonos ordinátájú pontok mértani helye (hiperciklus) a P-modellen egy-egy az egyenest modellező e  illetve a hiperciklust modellező h körív lesz, amelyek metszéspontja adja az (x,y) pontpár P-modellbeli P pontját, illetve ennek az O középpontú Descartes-féle koordinátarendszerben vett  koordinátáit. amelyeket tehát a  és r adatokból kell meghatároznunk.

Az ábra jelöléseit használva kapjuk az e és h körök egyenleteit:

   ahol 

  ahol 

Az is teljesül, hogy  , mert s merőleges a k alapkörre, és  mert h átellenes pontokban metszi k -t.

 Ezeket az összefüggéseket kihasználva az e és h körök hatványvonalára a  egyenletet kapjuk.

Másrészt, mivel  az O és P pont egyaránt illeszkedik a  szakasz Thalész - körére, így  és az  szögek egyenlők. Ebből: 

Ezekből némi számolással kapjuk, hogy

 , másrészt 

Figyelembe véve, hogy mind a  mind a kifejezés szorzótényezőként tartalmazza r -t, képleteink tovább egyszerűsíthetők:

 ,  , ahol, mint
korábban láttuk: . (Itt r az alapkör sugarának, e  az OE  szakasznak az euklídeszi mértékét jelöli.)
 

Eredményeinket alkalmazva lerajzoltuk néhány közismert függvény (az  ;  ;  ;  ;  ) képét ebben a koordinátarendszerben. Tanulmányozhatjuk, hogy az így kapott grafikonok attól függően közelítik meg jobban, vagy kevésbé az ismert alakjukat, hogy mekkorának választjuk az egységet az alapkör sugarához képest.

<<<<